题目内容
 如图,小亮用一个两个锐角分别为30°和60°的三角尺测量一棵树的高度,已知他与树之间的距离AE=8.0m,∠DAE=30°,眼睛与地面的距离AB为1.5m,那么这棵树的高度CD(精确到0.1m)大约为
如图,小亮用一个两个锐角分别为30°和60°的三角尺测量一棵树的高度,已知他与树之间的距离AE=8.0m,∠DAE=30°,眼睛与地面的距离AB为1.5m,那么这棵树的高度CD(精确到0.1m)大约为
- A.4.5m
- B.5.5m
- C.6.1m
- D.15.4m
C
分析:易得CE=AB,利用30°的正切值可求得DE的长,相加即为树的高度.
解答:∵AE=8cm,∠DAE=30°,
∴DE=AE•tan30°= ,
,
∴CD=CE+DE=1.5+ ≈6.1( m).
≈6.1( m).
故选C.
点评:考查三角函数的运用,关键是得到和所求线段相关的线段的长度.
分析:易得CE=AB,利用30°的正切值可求得DE的长,相加即为树的高度.
解答:∵AE=8cm,∠DAE=30°,
∴DE=AE•tan30°=
 ,
,∴CD=CE+DE=1.5+
 ≈6.1( m).
≈6.1( m).故选C.
点评:考查三角函数的运用,关键是得到和所求线段相关的线段的长度.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,小亮用一个两个锐角分别为30°和60°的三角尺测量一棵树的高度,已知他与树之间的距离AE=8.0m,∠DAE=30°,眼睛与地面的距离AB为1.5m,那么这棵树的高度CD(精确到0.1m)大约为( )
如图,小亮用一个两个锐角分别为30°和60°的三角尺测量一棵树的高度,已知他与树之间的距离AE=8.0m,∠DAE=30°,眼睛与地面的距离AB为1.5m,那么这棵树的高度CD(精确到0.1m)大约为( )| A、4.5m | B、5.5m | C、6.1m | D、15.4m |
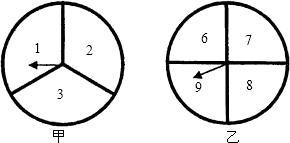
 小宁和小亮用如图所示的两个转盘做游戏,游戏规则为:转动两个转盘各一次,若转盘(1)的指针所指向区域的数字是转盘(2)的指针所指向区域的数字的整数倍,则小宁胜,否则小亮胜(若转盘指针指在分界线上,就重转一次),这个游戏对双方公平吗?为什么?如果不公平,请设计一个公平的游戏,并说明公平的理由.(要求用列表或树状图解答)
小宁和小亮用如图所示的两个转盘做游戏,游戏规则为:转动两个转盘各一次,若转盘(1)的指针所指向区域的数字是转盘(2)的指针所指向区域的数字的整数倍,则小宁胜,否则小亮胜(若转盘指针指在分界线上,就重转一次),这个游戏对双方公平吗?为什么?如果不公平,请设计一个公平的游戏,并说明公平的理由.(要求用列表或树状图解答)