题目内容
 已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数
已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数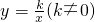 在第一象限内的交点.
在第一象限内的交点.
(1)求点A的坐标及k的值;
(2)试在x轴上确定一点B,使CB=CA,求出点B的坐标.
解: (1)∵点A(1,n)在y=2x+1的图象上,
(1)∵点A(1,n)在y=2x+1的图象上,
∴2+1=n,即n=3,
∴A点坐标为(1,3),
把点A(1,3)代入 得k=1×3=3;
得k=1×3=3;
(2)如图,作AD⊥y轴于D,
把x=0代入y=2x+1得y=1,
∴C点坐标为(0,1),
∴OC=1,
∵A点坐标为(1,3),
∴OD=3,AD=1,
∴CD=OD-OC=2,
在Rt△ADC中,CA= =
= ,
,
∵CB=CA,
∴CB= ,
,
设B点坐标为(x,0),
在Rt△OBC中,∵OB2+OC2=BC2,
∴x2+12=( )2,
)2,
解得x1=2,x2=-2,
∴B点坐标为(2,0)或(-2,0).
分析:(1)先把A(1,n)代入一次函数解析式求出n,确定A点坐标,然后把A点坐标代入y= 可求出k的值;
可求出k的值;
(2)作AD⊥y轴于D,先确定C点坐标(0,1),再利用勾股定理计算出CA= ,则CB=
,则CB= ,设B点坐标为(x,0),在Rt△OBC中,根据勾股定理可得到x2+12=(
,设B点坐标为(x,0),在Rt△OBC中,根据勾股定理可得到x2+12=( )2,然后解方程求出x即可得到B点坐标.
)2,然后解方程求出x即可得到B点坐标.
点评:本题考查了反比例函数的综合题:两个函数图象的交点坐标满足两函数解析式;会利用坐标表示线段的长和运用勾股定理进行计算.
 (1)∵点A(1,n)在y=2x+1的图象上,
(1)∵点A(1,n)在y=2x+1的图象上,∴2+1=n,即n=3,
∴A点坐标为(1,3),
把点A(1,3)代入
 得k=1×3=3;
得k=1×3=3;(2)如图,作AD⊥y轴于D,
把x=0代入y=2x+1得y=1,
∴C点坐标为(0,1),
∴OC=1,
∵A点坐标为(1,3),
∴OD=3,AD=1,
∴CD=OD-OC=2,
在Rt△ADC中,CA=
 =
= ,
,∵CB=CA,
∴CB=
 ,
,设B点坐标为(x,0),
在Rt△OBC中,∵OB2+OC2=BC2,
∴x2+12=(
 )2,
)2,解得x1=2,x2=-2,
∴B点坐标为(2,0)或(-2,0).
分析:(1)先把A(1,n)代入一次函数解析式求出n,确定A点坐标,然后把A点坐标代入y=
 可求出k的值;
可求出k的值;(2)作AD⊥y轴于D,先确定C点坐标(0,1),再利用勾股定理计算出CA=
 ,则CB=
,则CB= ,设B点坐标为(x,0),在Rt△OBC中,根据勾股定理可得到x2+12=(
,设B点坐标为(x,0),在Rt△OBC中,根据勾股定理可得到x2+12=( )2,然后解方程求出x即可得到B点坐标.
)2,然后解方程求出x即可得到B点坐标.点评:本题考查了反比例函数的综合题:两个函数图象的交点坐标满足两函数解析式;会利用坐标表示线段的长和运用勾股定理进行计算.

练习册系列答案
相关题目