题目内容
在△ABC中，∠B是钝角，AB=6，CB=8，则AC的范围是
- A.8＜AC＜10
- B.8＜AC＜14
- C.2＜AC＜14
- D.10＜AC＜14
D
分析：要求AC的范围，就要确定对应角的范围，当∠B=90°时，根据勾股定理计算AC的长度，根据钝角大于90°和三角形两边之和大于第三边，可以确定AC的范围．
解答：根据三角形两边之和大于第3边，两边之差小于第3边，可以确定AC的范围为2＜AC＜14，
又因为当∠B为直角时，AC=
=10，
而题目中给出的∠B为钝角，所以AC＞10，
整理得：AC的范围为10＜AC＜14．
故选D．
点评：本题考查的是三角形的三边关系，合理的运用勾股定理确定第3边的范围．
分析：要求AC的范围，就要确定对应角的范围，当∠B=90°时，根据勾股定理计算AC的长度，根据钝角大于90°和三角形两边之和大于第三边，可以确定AC的范围．
解答：根据三角形两边之和大于第3边，两边之差小于第3边，可以确定AC的范围为2＜AC＜14，
又因为当∠B为直角时，AC=
=10，而题目中给出的∠B为钝角，所以AC＞10，
整理得：AC的范围为10＜AC＜14．
故选D．
点评：本题考查的是三角形的三边关系，合理的运用勾股定理确定第3边的范围．
练习册系列答案
相关题目
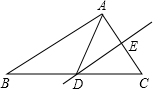如图所示，在△ABC中，DE是AC的中垂线，AE=3cm，△ABD得周长为13cm，则△ABC的周长是
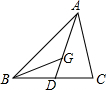如图，在△ABC中，AD是中线，G是重心，
如图在△ABC中，AD是BC边上的高，BE平分∠ABD，交AD于E．已知∠BED=60°，∠BAC=50°，则∠C=（ ）