题目内容
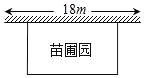
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园，其中一边靠墙，另外三边周长为 30 米的篱笆 围成．已知墙长为 18 米（如图所示），设这个苗圃园垂直于墙的一边的长为 x 米，若平行于墙的一边长不小 于 8 米，这个苗圃园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由．
【答案】最大值是
m2,最小值是88m2,理由见解析.
【解析】
由“平行于墙的一边长不小于8米、墙长为18米”可得x的范围，根据矩形的面积公式得出S关于x的函数解析式，配方成顶点式，利用二次函数的性质可得最值情况．
解：设这个苗圃园垂直于墙的一边的长为x米，则平行于墙的一边长为30-2x米，
根据题意得
∵S=x（30-2x）=-2x2+30x=-2 
8≤30-2x≤18，
解得：6≤x≤11，
∴当x＞
时，S随x的增大而减小，
∴当x=7.5时，S最大值=；
当x=11时，S最小值=11×（30-22）=88．
激活思维优加课堂系列答案
活力试卷系列答案
课课优能力培优100分系列答案
【题目】中华文化历史悠久，包罗万象．某校为了加强学生对中华传统文化的认识和理解，营造校园文化氛围，举办了“弘扬中华传统文化，做新时代的中学生”的知识竞赛．以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析，成绩如下：
七年级： 76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
八年级： 74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
（1）根据上面的数据，将下列表格补充完整，整理、描述数据：
|
|
|
|
| |
七年级 | 1 | 2 | 6 | ||
八年级 | 0 | 1 | 10 | 1 | 8 |
（说明：成绩90分及以上为优秀，60分以下为不合格）分析数据：
年级 | 平均数 | 中位数 | 众数 |
七年级 | 84 | 88.5 | |
八年级 | 84.2 | 74 |
（2）为调动学生学习传统文化的积极性，七年级根据学生的成绩制定了奖励标准，凡达到或超过这个标准的学生将获得奖励．如果想让一半左右的学生能获奖，应根据______来确定奖励标准比较合适．（填“平均数”、“众数”或“中位数”）；
（3）若八年级有800名学生，试估计八年级学生成绩优秀的人数；
【题目】2018年非洲猪瘟疫情暴发后，专家预测，2019年我市猪肉售价将逐月上涨，每千克猪肉的售价y1（元）与月份x（1≤x≤12，且x为整数）之间满足一次函数关系，如下表所示．每千克猪肉的成本y2（元）与月份x（1≤x≤12，且x为整数）之间满足二次函数关系，且3月份每千克猪肉的成本全年最低，为9元，如图所示．
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |
（1）求y1与x之间的函数关系式．
（2）求y2与x之间的函数关系式．
（3）设销售每千克猪肉所获得的利润为w（元），求w与x之间的函数关系式，哪个月份销售每千克猪肉所第获得的利润最大？最大利润是多少元？
