题目内容

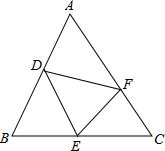已知：如图，在△ABC中，D为AB的中点，E、F分别为BC、AC边上的点．请你判断一下S_△DEF与S_△ADF+S_△BDE的大小关系，并证明．

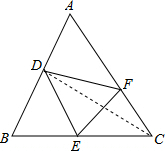解：S_△DEF≤S_△ADF+S_△BDE．
理由如下：连接CD，设 $\text{[math]}$ =x， $\text{[math]}$ =y，（0≤x≤1，0≤y≤1），△ABC的面积=S，
∵D为AB的中点，
∴S_△ACD=S_△BCD= $\text{[math]}$ S_△ABC= $\text{[math]}$ S，
又∵S_△ADF=（1-y）S_△ACD=（1-y）• $\text{[math]}$ S，
S_△BDE=（1-x）S_△BCD=（1-x）• $\text{[math]}$ S，
∴S_△ADF+S_△BDE=（1-y）• $\text{[math]}$ S+（1-x）• $\text{[math]}$ S=（2-x-y）• $\text{[math]}$ S，
又∵S_△CEF=xy•S，
∴S_△DEF=S-（2-x-y）• $\text{[math]}$ S-S•xy= $\text{[math]}$ S（x+y-2xy），
∴（S_△ADF+S_△BDE）-S_△DEF=（2-x-y）• $\text{[math]}$ S- $\text{[math]}$ S（x+y-2xy）= $\text{[math]}$ S（2-2x-2y+2xy）=S（1-x-y+xy）=S（1-x）（1-y），
∵0≤x≤1，0≤y≤1，
∴S（1-x）（1-y）≥0恒成立，
当点E与B重合或点F与A重合时，等号成立，
所以，S_△DEF≤S_△ADF+S_△BDE．
分析：连接CD，设 $\text{[math]}$ =x， $\text{[math]}$ =y，△ABC的面积=S，根据等底等高的三角形的面积相等，等高的三角形的面积的比等于底边的比分别表示出△ACD、△BCD的面积，再表示出△ADF、△BDE的面积以及△CEF的面积，
点评：本题考查了三角形的面积，主要利用了等底等高的三角形的面积相等，等高的三角形的面积等于底边的比，用△ABC的面积表示出图中各三角形的面积是解题的关键，也是本题的难点．