题目内容

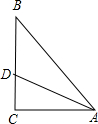已知，如图△ABC中，∠C=90°，AD平分∠BAC，CD= $数学公式$ ，BD=2 $数学公式$ ，求平分线AD的长，AB，AC的长，外接圆的面积，内切圆的面积．

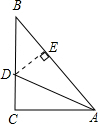解：设AC的长为x，过D作DE垂直AB于点E，
则BC=BD+DC= $\text{[math]}$ ，AB= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
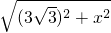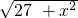∵AD平分∠BAC，DC⊥AC，DE⊥AB，
∴DC=DE，
∵Rt△BED∽Rt△BCA，
∴ $\text{[math]}$ ，
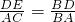即 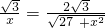$\text{[math]}$ ?4x²=27+x²，
解得x=3或x=-3（不合题意舍去），
AD= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
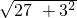∴AB= $\text{[math]}$ =6，
显然可知AB为Rt△ABC的外接圆的直径，
∴Rt△ABC外接圆的面积=π•3²=9π，
Rt△ABC内切圆的半径= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ，
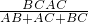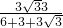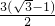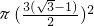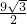Rt△ABC内切圆的面积= $\text{[math]}$ =（9- $\text{[math]}$ ）π．
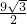答：平分线AD的长为 $\text{[math]}$ ，AB的长为6，AC的长3，外接圆的面积为9π，内切圆的面积是（9- $\text{[math]}$ ）π．
分析：首先设AC的长为x，过D作DE垂直AB于点E．根据角平分线的性质定理及相似三角形的性质，可得到关系式4x²=27+x²，解得x即为AC的长，再利用勾股定理求得AB、AD的长．根据直角三角形内切圆的性质、外接圆的性质，求得其半径，根据圆的面积计算公式即可求出结果．
点评：本题考查三角形内切圆与内心、勾股定理、角平分线的性质、三角形外接圆与外心、相似三角形的性质．解决本题的关键是首先设AC为x，通过作辅助线DE建立起边间的关系，列出关系式4x²=27+x²，使问题得解．