题目内容
（2012•保康县模拟）如图，⊙O的直径AB=12，弦CD⊥AB于M，且M是半径OB的中点，则CD的长是6
| 3 |
6
（结果保留根号）．| 3 |
分析：连OC，易得OC=6，OM=3，根据勾股定理可计算出CM=3
，由于CD⊥AB，根据垂径定理得到CM=
CD，即可计算出CD的长．
| 3 |
| 1 |
| 2 |
解答：解：连OC，如图，
∵直径AB=12，M是半径OB的中点，
∴OC=6，OM=3，
在Rt△OCM中，CM=
=
=3
，
∵CD⊥AB，
∴CM=
CD，
∴CD=2CM=6
．
故答案为6
．
∵直径AB=12，M是半径OB的中点，
∴OC=6，OM=3，
在Rt△OCM中，CM=
| OC2-OM2 |
| 62-32 |
| 3 |
∵CD⊥AB，
∴CM=
| 1 |
| 2 |
∴CD=2CM=6
| 3 |
故答案为6
| 3 |
点评：本题考查了垂径定理：垂直于弦的直径平分弦，并且平分弦所对的弧．也考查了勾股定理．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
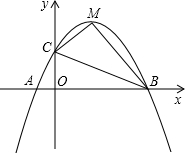（2012•保康县模拟）如图，已知抛物线y=