题目内容
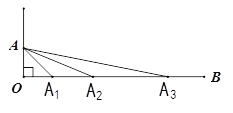
【题目】如图,已知![]() ,点
,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,点
上,点![]() 绕点
绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线
落在射线![]() 上,…,连接
上,…,连接![]() 、
、![]() 、
、![]() …,以此作法,则
…,以此作法,则![]() =______度.(用含
=______度.(用含![]() 的代数式表示,
的代数式表示, ![]() 为正整数)
为正整数)
【答案】![]()
【解析】因为点A绕点O顺时针旋转后的对应点![]() 落在射线OB上,
落在射线OB上,
∴OA=O![]() ,∴∠A
,∴∠A![]() O=
O=![]() ,∵点A绕点
,∵点A绕点![]() 顺时针旋转后的对应点
顺时针旋转后的对应点![]() 落在射线OB上,
落在射线OB上,
∴![]() =
=![]() ,∴
,∴![]() ,
,
∵点A绕点![]() 顺时针旋转后的对应点,
顺时针旋转后的对应点, ![]() 落在射线OB上,∴
落在射线OB上,∴ ![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
故答案为: ![]() .
.
点睛:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心所连线段间的夹角为旋转角。三要素中只要任意改变一个,图形就会不一样。 旋转变换是由一个图形改变为另一个图形,在改变过程中,原图上所有的点都绕一个固定的点换同一方向,转动同一个角度

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目