题目内容
【题目】在平面直角坐标系中,直线![]() 与x轴交于点B,与y轴交于点C,二次函数
与x轴交于点B,与y轴交于点C,二次函数![]() 的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
的图象经过点B,C两点,且与x轴的负半轴交于点A,动点D在直线BC下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图1,连接DC,DB,设△BCD的面积为S,求S的最大值;
(3)如图2,过点D作DM⊥BC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠ABC的2倍?若存在,直接写出点D的横坐标;若不存在,请说明理由.

【答案】(1)二次函数的表达式为:![]() ;(2)4;(3)
;(2)4;(3)![]() 或
或![]() .
.
【解析】
(1)先求得点B、C的坐标,再代入![]() 求得b、c的值,即可得二次函数的表达式;(2)过点
求得b、c的值,即可得二次函数的表达式;(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,设
,设![]() ,则
,则![]() .用含有a的代数式表示出
.用含有a的代数式表示出![]() 的长,再根据
的长,再根据![]() 得到S与a的二次函数关系,利用二次函数的性质即可解答;(3)在x轴上取点K,使CK=BK,则∠OKC=2∠ABC,过点B作BQ∥MD交CD延长线于点Q,过点Q作QH⊥x轴于点H,分∠DCM=∠QCB=2∠ABC和∠CDM=∠CQB=2∠ABC两种情况求点D的横坐标即可.
得到S与a的二次函数关系,利用二次函数的性质即可解答;(3)在x轴上取点K,使CK=BK,则∠OKC=2∠ABC,过点B作BQ∥MD交CD延长线于点Q,过点Q作QH⊥x轴于点H,分∠DCM=∠QCB=2∠ABC和∠CDM=∠CQB=2∠ABC两种情况求点D的横坐标即可.
(1)直线![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴![]() ,
,![]() .
.
∵二次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,
两点,
∴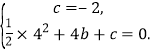 解得
解得
∴二次函数的表达式为:![]() .
.
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
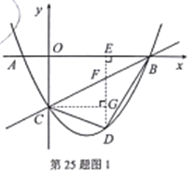
依题意设![]() ,则
,则![]() .
.
其中![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
∵![]() ,∴抛物线开口向下.
,∴抛物线开口向下.
又∵![]() ,
,
∴当![]() 时,
时,![]() 有最大值,
有最大值,![]() ;
;
(3)![]() 或
或![]()
在![]() 轴上取点
轴上取点![]() ,使
,使![]() ,则
,则![]() .
.
过点![]() 作
作![]() ∥
∥![]() 交
交![]() 延长线于点
延长线于点![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
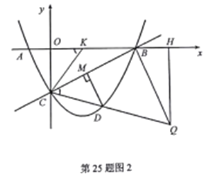
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,解得
,解得![]() .∴
.∴![]() .
.
当![]() 时,
时,
∴![]() .
.
∴![]() .
.
易证![]() ∽
∽![]() .
.
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴直线![]() 的函数表达式为:
的函数表达式为:![]() .
.
由![]() ,解得:
,解得:![]() ,
,![]() (舍).
(舍).
∴![]() 点的横坐标为2.
点的横坐标为2.
②当![]() 时,方法同①,可确定点
时,方法同①,可确定点![]() 的横坐标为
的横坐标为![]() .
.

练习册系列答案
相关题目