��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У���A��10��0������OAΪֱ���ڵ�һ����������Բ��BΪ��Բ��һ�㣬����AB���ӳ���C��ʹBC=AB����C��CD �� x���ڵ�D,���߶�OB�ڵ�E����֪CD=8,�����߾���O��E��A���㡣
��1�� ��OBA= �㣮
��2�� �������ߵĺ�������ʽ��
��3�� ��PΪ��������λ�ڵ�һ�����ڵ�һ�����㣬��P��O��A��EΪ������ı����������S����Sȡ��ֵʱ����Ӧ�ĵ�P����ֻ��3����
 |
(1)��OBA=90��
(2)����OC����ͼ��ʾ��
����(1)֪OB �� AC����AB=BC��
 ��OB�ǵĴ�ֱƽ���ߣ�
��OB�ǵĴ�ֱƽ���ߣ�
��OC=OA=10��
��Rt��OCD��OC=10��CD=8����OD=6��
��C(6��8)��B(8��4)
��OB����ֱ�ߵĺ�����ϵΪy= x��
x��
��E��ĺ�����Ϊ6����E��������Ϊ3
��E(6,3)��
�����߹�O(0��0)��E(6,3) ��A(10��0)
����������ߵĺ�����ϵʽΪy=ax(x��10)����E����������
3=6a(6��10)�����a=��
��������ߵĺ�����ϵʽΪy=�� x(x��10)����y=��
x(x��10)����y=�� x²��
x²�� x��
x��
(4) ���P(p���� p²��
p²�� p)
p)
�� ����P��CD����࣬�ӳ�OP��CD��Q������ͼ��
OP����ֱ�ߺ�����ϵʽΪ��y=(�� p��
p�� )x
)x
�൱x=6ʱ��y= ����Q��������Ϊ
����Q��������Ϊ ��
��
��QE= ��3=
��3= ��
��
 S�ı���POAE
S�ı���POAE
= S��OAE ��S��OPE
= S��OAE ��S��OQE��S��PQE
=  · OA ·DE ��
· OA ·DE �� · QE · Px
· QE · Px
= ��10��3��
��10��3�� ·(
·( )· p
)· p
=
�� ����P��CD���Ҳ࣬�ӳ�AP��CD��Q������ͼ��
P
 (p����
(p���� p²��
p²�� p)��A(1
p)��A(1 0,0)
0,0)
����AP����ֱ�߷���Ϊ��y=kx��b����P��A�������ã�
 �����
����� ��
��
��AP����ֱ�߷���Ϊ��y= x��
x�� ��
��
�൱x=6ʱ��y= · 6��
· 6�� =
= P����Q��������Ϊ
P����Q��������Ϊ P��
P��
��QE= P��3��
P��3��
��S�ı���POAE
= S��OAE ��S��APE
 = S��OAE ��S��AQE ��S��PQE
= S��OAE ��S��AQE ��S��PQE
= ·OA ·DE ��
·OA ·DE �� · QE·DA��
· QE·DA�� · QE·(Px ��6)
· QE·(Px ��6)
= ��10��3��
��10��3�� · QE ·(DA��Px ��6)
· QE ·(DA��Px ��6)
=15�� ·(
·( p��3)·(10��p)
p��3)·(10��p)
=
=
�൱P��CD�Ҳ�ʱ���ı���POAE��������ֵΪ16����ʱ��P��λ�þ�һ����
�� =16����ã�p=3 ��
=16����ã�p=3 ��  ��
��
�൱P��CD���ʱ���ı���POAE���������16�Ķ�ӦP��λ����������
����֪����P��O��A��EΪ������ı������S����16ʱ����Ӧ�ĵ�P����ֻ��3����

 �����ߴ���ϵ�д�
�����ߴ���ϵ�д�
 ��AD=10��DC=3����ABD=60�㣬��AB= ʱ���ı���BFCE�����Σ�
��AD=10��DC=3����ABD=60�㣬��AB= ʱ���ı���BFCE�����Σ�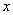 ǧ�ף������Ϊ15.5Ԫ����ô
ǧ�ף������Ϊ15.5Ԫ����ô �ݵ���λ��Ϊ
�ݵ���λ��Ϊ 