题目内容
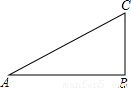
如图，小王在陆地上从A地经B地到达C地总行程是14千米，这里的∠ABC为直角，且∠BAC的正切值为0.75．那么小王乘海轮从A地直接到C地的最短距离是多少千米？
分析：由题意可知，在Rt△ABC中，∠C=90°，AB+BC=14，假设AB=X，则BC=14-X，根据∠BAC的正切值为0.75，得到
=0.75，代入可求得X的值，再由勾股定理求得AC的值．
| BC |
| AB |
解答：解：设AB=x，则BC=14-x，在Rt△ABC中，tan∠BAC=
=
=0.75，
解得x=AB=8，
∴BC=6，
AC=
=10千米，
即从A到C的最短距离为10千米．
| BC |
| AB |
| 14-x |
| x |
解得x=AB=8，
∴BC=6，
AC=
| AB2+BC2 |
即从A到C的最短距离为10千米．
点评：主要考查了直角三角形，只要我们把实际问题抽象到解直角三角形中，即可求出．
练习册系列答案
阅读快车系列答案
相关题目
如图，小王在陆地上从A地经B地到达C地总行程是14千米，这里的∠ABC为直角，且∠BAC的正切值为0.75．那么小王乘海轮从A地直接到C地的最短距离是多少千米？
