题目内容
【题目】如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y= 
（k＞0，x＞0）的图象上，点D的坐标为（ 
，2）．
（1）求k的值；
（2）若将菱形ABCD沿x轴正方向平移，当菱形的一个顶点恰好落在函数y= （k＞0，x＞0）的图象上时，求菱形ABCD平移的距离．
【答案】
（1）
解：作DE⊥BO，DF⊥x轴于点F，
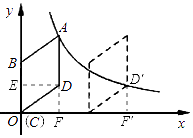
∵点D的坐标为（ 
，2），
∴DO=AD=3，
∴A点坐标为：（ ，5），
∴k=5 ；
（2）
解：∵将菱形ABCD向右平移，使点D落在反比例函数y= 
（x＞0）的图象上D′，
∴DF=D′F′=2，
∴D′点的纵坐标为2，设点D′（x，2）
∴2= 
，解得x= 
，
∴FF′=OF′﹣OF= ﹣ = 
，
∴菱形ABCD平移的距离为 ，
同理，将菱形ABCD向右平移，使点B落在反比例函数y= （x＞0）的图象上，
菱形ABCD平移的距离为 
，
综上，当菱形ABCD平移的距离为 或 
时，菱形的一个顶点恰好落在函数图象上．
【解析】（1）根据菱形的性质和D的坐标即可求出A的坐标，代入求出即可；（2）B和D可能落在反比例函数的图象上，根据平移求出即可．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
