Question

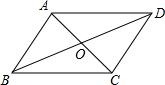如图所示，?ABCD的两条对角线相交于点O，OA，OB，AB的长分别为5cm，13cm，12cm，则CD=

12cm

，BD=

26cm

，AC=

10cm

，∠ACD的度数是

90°

．

Answer 1

分析：由?ABCD的两条对角线相交于点O，OA，OB，AB的长分别为5cm，13cm，12cm，根据平行四边形的性质，可求得CD，BD，AC的长，又由勾股定理的逆定理，可得△OCD是直角三角形．

解答：解：∵四边形ABCD是平行四边形，且OA，OB，AB的长分别为5cm，13cm，12cm，
∴CD=AB=12cm，BD=2OB=26cm，AC=2OA=10cm，OD=OB=13cm，OC=OA=5cm，
∴OC²+CD²=OD²，
∴∠OCD=90°，
即∠ACD=90°．
故答案为：12cm，26cm，10cm，90°．

点评：此题考查了平行四边形的性质以及勾股定理的逆定理．此题难度适中，注意掌握数形结合思想的应用．