题目内容
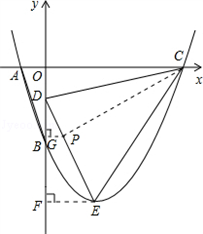
如图,直线y=﹣3x﹣3分别交x轴、y轴于A、B两点,△AOB绕点O按逆时针方向旋转90°后得到△DOC,抛物线y=ax2+bx+c经过A、B、C三点。
(1)填空:A( _________ , _________ )、B( _________ , _________ )、C( _________ , _________ );(2)求抛物线的函数关系式;
(3)E为抛物线的顶点,在线段DE上是否存在点P,使得以C、D、P为顶点的三角形与△DOC相似?若存在,请求出点P的坐标;若不存在,请说明理由。
(1)填空:A( _________ , _________ )、B( _________ , _________ )、C( _________ , _________ );(2)求抛物线的函数关系式;
(3)E为抛物线的顶点,在线段DE上是否存在点P,使得以C、D、P为顶点的三角形与△DOC相似?若存在,请求出点P的坐标;若不存在,请说明理由。

| 解:(1)直线y=﹣3x﹣3中, x=0,则y=﹣3; y=0,则x=﹣1; ∴A(﹣1,0),B(0,﹣3); 根据旋转的性质知:OC=OB=3,即C(3,0); ∴A(﹣1,0),B(0,﹣3),C(3,0); (2)∵抛物线y=ax2+bx+c经过B点, ∴c=﹣3; 又∵抛物线经过A,C两点, ∴ 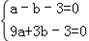 , ,解得 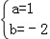 ; ;∴y=x2﹣2x﹣3; (3)过点E作EF⊥y轴垂足为点F; 由(2)得y=x2﹣2x﹣3=(x﹣1)2﹣4 ∴E(1,﹣4), ∵tan∠EDF=  ,tan∠DCO= ,tan∠DCO= ; ;∴∠EDF=∠DCO ∵∠DCO+∠ODC=90°, ∴∠EDF+∠ODC=90°; ∴∠EDC=90°, ∴∠EDC=∠DOC; ①当 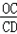 = =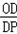 时,△ODC∽△DPC,则 时,△ODC∽△DPC,则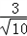 = =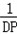 , ,∴DP= 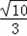 过点P作PG⊥y轴,垂足为点G; ∵tan∠EDF=  = =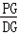 , ,∴设PG=x,则DG=3x 在Rt△DGP中,DG2+PG2=DP2, ∴9x2+x2= 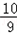 , ,∴x1=  ,x2=﹣ ,x2=﹣ (不合题意,舍去) (不合题意,舍去)又∵OG=DO+DG=1+1=2, ∴P(  ,﹣2); ,﹣2);②当 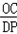 = =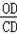 时,△ODC∽△DCP,则 时,△ODC∽△DCP,则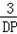 = =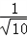 , ,∴DP=3 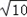 ; ;∵DE= 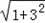 = =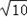 , ,∴DP=3  (不合题意,舍去) (不合题意,舍去)综上所述,存在点P,使得以C、D、P为顶点的三角形与△DOC相似, 此时点P的坐标为P(  ,﹣2)。 ,﹣2)。 |
 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图:直线y=-3x+6与y轴交于点A,与直线y=2x+1交于点B,且直线y=2x+1与x轴交于点C,则△ABC的面积为
如图:直线y=-3x+6与y轴交于点A,与直线y=2x+1交于点B,且直线y=2x+1与x轴交于点C,则△ABC的面积为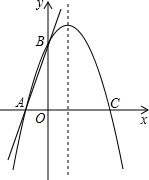 如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0). (2012•双柏县二模)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0).
(2012•双柏县二模)如图,直线y=3x+3交x轴于A点,交y轴于B点,过A、B两点的抛物线交x轴于另一点C(3,0). ,0).
,0).