题目内容
 如图,已知PA,PB为⊙O的切线,A,B为切点,C为⊙O上一点,∠ACB=70°,则∠P的度数是
如图,已知PA,PB为⊙O的切线,A,B为切点,C为⊙O上一点,∠ACB=70°,则∠P的度数是
- A.20°
- B.40°
- C.70°
- D.35°
B
分析:首先连接OA,OB,由PA,PB为⊙O的切线,根据切线的性质,即可得∠OAP=∠OBP=90°,又由圆周角定理,可求得∠AOB的度数,继而可求得答案.
解答: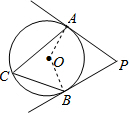 解:连接OA,OB,
解:连接OA,OB,
∵PA,PB为⊙O的切线,
∴∠OAP=∠OBP=90°,
∵∠ACB=70°,
∴∠AOB=2∠P=140°,
∴∠P=360°-∠OAP-∠OBP-∠AOB=40°.
故选B.
点评:此题考查了切线的性质与圆周角定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
分析:首先连接OA,OB,由PA,PB为⊙O的切线,根据切线的性质,即可得∠OAP=∠OBP=90°,又由圆周角定理,可求得∠AOB的度数,继而可求得答案.
解答:
 解:连接OA,OB,
解:连接OA,OB,∵PA,PB为⊙O的切线,
∴∠OAP=∠OBP=90°,
∵∠ACB=70°,
∴∠AOB=2∠P=140°,
∴∠P=360°-∠OAP-∠OBP-∠AOB=40°.
故选B.
点评:此题考查了切线的性质与圆周角定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
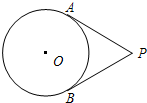 如图,已知PA、PB都是⊙O的切线,A、B为切点,且∠APB=60°.若点C是⊙O异于A、B的任意一点,则∠ACB=( )
如图,已知PA、PB都是⊙O的切线,A、B为切点,且∠APB=60°.若点C是⊙O异于A、B的任意一点,则∠ACB=( )| A、60° | B、120° | C、60°或120° | D、不能确定 |
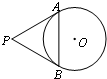 9、如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是
9、如图,已知PA,PB分别切⊙O于点A、B,∠P=60°,PA=8,那么弦AB的长是 5、如图,已知PA、PB切⊙O于点A、B,OP交AB于C,则图中能用字母表示的直角共有( )个.
5、如图,已知PA、PB切⊙O于点A、B,OP交AB于C,则图中能用字母表示的直角共有( )个. 如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC的大小是( )
如图,已知PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC的大小是( ) (2012•锦州二模)如图,已知PA、PB是⊙O的两条切线,A、B是切点,连接OP.
(2012•锦州二模)如图,已知PA、PB是⊙O的两条切线,A、B是切点,连接OP.