题目内容
一位警察奉命追击一名正在向南偏西30°方向逃蹿的罪犯，如图，警察的位置在点A（120，120
+30），罪犯的位置在点B（-180，-180
），图中的阴影部分表示一条东西走向宽30米的河道，如果警察追击的速度是8米/秒，罪犯逃跑的速度是7.5米/秒，且警察
经过河道时正好有一座垂直于河道两岸的桥，要想在最短的时间内追上罪犯，警察至少要追击的时间为（ ）
| 3 |
| 3 |
经过河道时正好有一座垂直于河道两岸的桥，要想在最短的时间内追上罪犯，警察至少要追击的时间为（ ）| A、19分钟 | B、20分钟 |
| C、21分钟 | D、22分钟 |
分析：根据轴对称确定最短路线问题，过点A作AD⊥河岸且使AD等于河岸的宽度30米，设t分钟在点E处追上罪犯，连接DE，则AD+DE为警察的路程，BE为罪犯的路程，过点D作河岸的平行线，过点E作河岸的垂线，相交于点F，然后表示出DE、DF、EF，再利用勾股定理列出方程求解即可．
解答：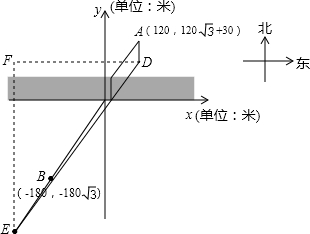
解：如图，过点A作AD⊥河岸且使AD=30米，
警察的速度为8×60=480米/分，
罪犯的速度为7.5×60=450米/分，
设t分钟在点E处追上罪犯，连接DE，
则DE=480t-30，
过点D作河岸的平行线，过点E作河岸的垂线，相交于点F，
∵罪犯沿向南偏西30°方向逃蹿，
∴DF=120+（180+
×450t）=225t+300，
EF=（120
+30-30）+180
+450×
t=225
t+300
，
在Rt△DEF中，DE2=DF2+EF2，
即（480t-30）2=（225t+300）2+（225
t+300
）2，
∴480t-30=2（225t+300），
解得t=21，
即警察至少需要21分钟追上罪犯．
故选C．
解：如图，过点A作AD⊥河岸且使AD=30米，警察的速度为8×60=480米/分，
罪犯的速度为7.5×60=450米/分，
设t分钟在点E处追上罪犯，连接DE，
则DE=480t-30，
过点D作河岸的平行线，过点E作河岸的垂线，相交于点F，
∵罪犯沿向南偏西30°方向逃蹿，
∴DF=120+（180+
| 1 |
| 2 |
EF=（120
| 3 |
| 3 |
| ||
| 2 |
| 3 |
| 3 |
在Rt△DEF中，DE2=DF2+EF2，
即（480t-30）2=（225t+300）2+（225
| 3 |
| 3 |
∴480t-30=2（225t+300），
解得t=21，
即警察至少需要21分钟追上罪犯．
故选C．
点评：本题考查了轴对称确定最短路线问题，坐标与图形性质，熟练掌握过河确定最短路线问题的方法是解题的关键，难点在于作辅助线构造成直角三角形并利用勾股定理列出方程．
练习册系列答案
相关题目