题目内容
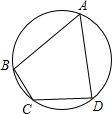 如图,圆内接四边形ABCD中,∠A=60°,∠B=90°,AD=3,CD=2,则BC=________.
如图,圆内接四边形ABCD中,∠A=60°,∠B=90°,AD=3,CD=2,则BC=________.
 -1
-1分析:由圆内接四边形ABCD的对角互补,得到∠D=180°-∠B=90°,延长AB和DC交于点E,∠A=60°,则∠E=30°,在直角三角形ADE中,ED=
 AD=3
AD=3 ,则EC=3
,则EC=3 -2;又在直角三角形ECB中,BC=
-2;又在直角三角形ECB中,BC= EC,这样就可求出BC.
EC,这样就可求出BC.解答:
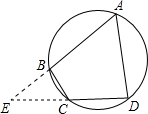 解:延长AB和DC交于点E,如图,
解:延长AB和DC交于点E,如图,∵四边形ABCD为圆内接四边形,∠B=90°,
∴∠D=180°-∠B=90°,
∵∠A=60°,
∴∠E=30°,
在直角三角形ADE中,
ED=
 AD,而AD=3,所以ED=
AD,而AD=3,所以ED= AD=3
AD=3 ,
,又∵CD=2,
∴EC=3
 -2;
-2;在直角三角形ECB中,
BC=
 EC=
EC= (3
(3 -2)=
-2)= -1.
-1.故答案为:
 -1.
-1.点评:本题考查了圆周角定理:在同圆和等圆中,同弧或等弧所对的圆周角相等,一条弧所对的圆周角是它所对的圆心角的一半.同时考查了圆内接四边形的性质和含30度的直角三角形的三边的关系为1:
 :2.
:2. 
练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 如图,圆内接四边形ABCD,AB=AD,∠BAD=60°,AC=2,则四边形ABCD的面积为( )
如图,圆内接四边形ABCD,AB=AD,∠BAD=60°,AC=2,则四边形ABCD的面积为( )| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
 11、如图,圆内接四边形ABCD的对角线AC,BD把四边形的四个内角分成八个角,这八个角中相等的角的对数至少有( )
11、如图,圆内接四边形ABCD的对角线AC,BD把四边形的四个内角分成八个角,这八个角中相等的角的对数至少有( )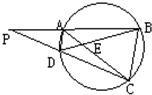 15、如图,圆内接四边形ABCD的BA,CD的延长线交于P,AC,BD交于E,则图中相似三角形有( )
15、如图,圆内接四边形ABCD的BA,CD的延长线交于P,AC,BD交于E,则图中相似三角形有( ) 2、已知:如图,圆内接四边形ABCD中,∠BAD=65°,则∠BCD=
2、已知:如图,圆内接四边形ABCD中,∠BAD=65°,则∠BCD= 已知:如图,圆内接四边形ABCD,过C点作对角线BD的平行线交AD的延长线于E点.
已知:如图,圆内接四边形ABCD,过C点作对角线BD的平行线交AD的延长线于E点.