Question

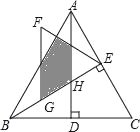
【题目】点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为AB，当A、B两点中有一点在原点时，不妨设点A在原点，如图甲，；当A、B两点都不在原点时，

①如图乙，点 A、B 都在原点的右边，；

②如图丙，点 A、B 都在原点的左边，；

③如图丁，点 A、B 在原点的两边，.

综上，数轴上A、B两点之间的距离.

回答下列问题：

数轴上表示- 2和 5 的两点之间的距离是________;

②数轴上表示 x 和 3 的两点分别是点 A 和 B ，如果，那么 x _______;

③当代数式取最小值时，相应的x的取值范围是_______.

④当代数式取最大值时，相应的x的取值范围是________.

Answer 1

【答案】①；②或；④

【解析】

①②直接根据数轴上两点之间的距离．代入数值运用绝对值即可求任意两点间的距离．
③根据绝对值的性质，可得到一个一元一次不等式组，通过求解，就可得出的取值范围．
④根据题意分三种情况：当时，当时，当时，分别求出方程的解即可．

①数轴上表示- 2和5 的两点之间的距离是：；

②根据绝对值的定义有：数轴上表示 x 和3 的两点的距离是

∵，∴，即

∴或

③根据绝对值的定义有：可表示为点到与两点距离之和，根据几何意义分析可知：
当时，有最小值．

④当代数式取最大值时，根据题意分三种情况：

当时，；

当时，

当时，

综上：代数式取最大值是7，此时