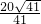题目内容
直角三角形三边的长分别是5，4，m，则此三角形斜边上的高为（ ）
分析：分两种情况讨论，①5为斜边，②5为直角边，分别求出三角形的面积，继而可得出此三角形斜边上的高．
解答：解：①若5为斜边，则m=
=3，
S=
×3×4=6，此三角形斜边上的高=
；
②若5为直角边，则m=
=
，
S=
×5×4=10，此三角形斜边上的高=
；
则此三角形斜边上的高为：
或
．
故选A．
| 52-42 |
S=
| 1 |
| 2 |
| 12 |
| 5 |
②若5为直角边，则m=
| 52+42 |
| 41 |
S=
| 1 |
| 2 |
20
| ||
| 41 |
则此三角形斜边上的高为：
| 12 |
| 5 |
20
| ||
| 41 |
故选A．
点评：本题考查了勾股定理的知识及三角形的面积，解答本题的关键是分类讨论，确定斜边，注意勾股定理的表达式．
练习册系列答案
相关题目
已知一直角三角形两边的长分别是3cm和4cm，则第三边的长为（ ）cm．
| A、5 | ||
B、5和
| ||
C、
| ||
| D、不能确定 |
或
