题目内容
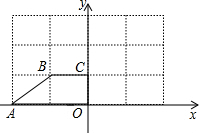
如图(1),在直角梯形OABC中,BC∥OA,∠OCB=90°,OA=6,AB=5,cos∠OAB=![]() .
.
(1)写出顶点A、B、C的坐标;
(2)如图(2),点P为AB边上的动点(P与A、B不重合),PM⊥OA,PN⊥OC,垂足分别为M,N.设PM=x,四边形OMPN的面积为y.
①求出y与x之间的函数关系式,并写出自变量x的取值范围;
②是否存在一点P,使得四边形OMPN的面积恰好等于梯形OABC的面积的一半?如果存在,求出点P的坐标;如果不存在,说明理由.

(1) A(6,0),B(3,4),C(0,4) (2)①![]() 0<x<4 ②存在P点(
0<x<4 ②存在P点(![]() ,2)
,2)

练习册系列答案
相关题目


 ),将直角梯.形OABC绕点O顺时针旋转90°后,点A、B、C分别落在点A′、B′、C′处.请你解答下列问题:
),将直角梯.形OABC绕点O顺时针旋转90°后,点A、B、C分别落在点A′、B′、C′处.请你解答下列问题: