Question

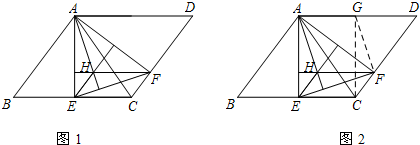
小杰遇到这样一个问题：如图1，在?ABCD中，AE⊥BC于点E，AF⊥CD于点F，连接EF，△AEF的三条高线交于点H，如果AC=4，EF=3，求AH的长．
小杰是这样思考的：要想解决这个问题，应想办法将题目中的已知线段与所求线段尽可能集中到同一个三角形中．他先后尝试了翻折、旋转、平移的方法，发现可以通过将△AEH平移至△GCF的位置（如图2），可以解决这个问题．
请你参考小杰同学的思路回答：
（1）图2中AH的长等于______

Answer 1

【答案】分析：（1）连接EG，先判定四边形AECG是矩形，然后根据矩形的对角线相等可得EG=AC，再根据平移可得GF⊥EF，然后在Rt△EFG中，利用勾股定理列式进行计算即可得解；
（2）根据（1）的计算，把AC、EF的长度代入进行计算即可得解．
解答：解：（1）如图，连接EG，
∵AE⊥BC于点E，△GCF由△AEH平移得到，
∴CG∥AE，
又∵?ABCD的边AD∥BC，AE⊥BC
∴四边形AECG是矩形，
∴EG=AC=4，
∵AH⊥EF，GF是由AH平移得到，
∴GF⊥EF，
在Rt△EFG中，GF===，
即AH=；

（2）根据（1）的计算，AH=GF==．
故答案为：，．
点评：本题考查了平行四边形的性质，勾股定理的应用，平移的性质，连接EG，证明出四边形AECG是矩形，从而得到EG=AC是解题的关键．