题目内容
| 类型 价格 | A型 | B型 |
| 进价（元/盏） | 40 | 65 |
| 标价（元/盏） | 60 | 100 |
（1）同学们，你知道聪聪购买了这两种台灯各多少盏吗？说明你的理由．
（2）在每种台灯销售利润不变的情况下，若老板要求：计划销售这批台灯的总利润不少于1400元，问至少需购进B种台灯多少盏？
根据题意，得
，解得：
；（2）设购进B型台灯m盏，则A型灯为50-m盏，
根据题意，得35m+20（50-m）≥1400，
解得，m≥
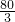；即，至少需购进B种台灯27盏；
答：A型台灯购进30盏，B型台灯购进20盏；要使销售这批台灯的总利润不少于
1400元，至少需购进B种台灯27盏．
分析：两种灯的总数为50，两种灯的进货款总和为2500元，列出二元一次方程组，求出两种灯的数量．再利用两种灯的总利润大于或等于1400元求出B型灯的数量范围．
点评：本题考查一元一次不等式在实际生活中的运用，本题是将现实生活中的事件与数学思想联系起来，解决问题的关键是读懂题意，依题意列出方程及不等式进行求解．
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案行驶中的汽车，在刹车后由于惯性的作用，还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”．为了测定某型号汽车的刹车性能(车速度不能超过140km/h)，对这种汽车进行测试，测得数据如下：
|
刹车时车速（km/h） |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
刹车距离（m） |
0 |
0.3 |
1.0 |
2.1 |
3.6 |
5.5 |
7.8 |
(1)以车速为x轴，以刹车距离为y轴，在坐标系中描出这些数据所表示的点，并用平滑的曲线连结这些点，得到函数的大致图像；
(2)观察图像，估计函数的类型．
(3)如果该函数解析式为
，若该型号汽车在国道上发生了一次交通事故，现场测得刹车距离为46.5m，请推测刹车时的速度．在事故发生时，汽车是超速行驶还是正常行驶？
行驶中的汽车，在刹车后由于惯性的作用，还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”．为了测定某型号汽车的刹车性能(车速度不能超过140km/h)，对这种汽车进行测试，测得数据如下：
|
刹车时车速（km/h） |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
|
刹车距离（m） |
0 |
0.3 |
1.0 |
2.1 |
3.6 |
5.5 |
7.8 |
(1)以车速为x轴，以刹车距离为y轴，在坐标系中描出这些数据所表示的点，并用平滑的曲线连结这些点，得到函数的大致图像；
(2)观察图像，估计函数的类型．
(3)如果该函数解析式为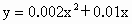
，若该型号汽车在国道上发生了一次交通事故，现场测得刹车距离为46.5m，请推测刹车时的速度．在事故发生时，汽车是超速行驶还是正常行驶？
Ⅰ、蜗牛壳上有条纹与无条纹的性状是由一对等位基因A和a控制的。研究人员调查了某地区的1000只蜗牛，对存活的个体数和被鸟捕食后剩下的蜗牛空壳数进行统计，得到数据如下表, 请回答下列问题：
| | 有条纹（显性） | 无条纹（隐性） | 合计 |
| 存活个体数 | 178 | 211 | 389 |
| 空壳数 | 332 | 279 | 611 |
| 合计 | 510 | 490 | 1000 |
⑵由表中数据可推断，壳上 （有条纹、无条纹）的蜗牛更易被鸟捕食。经多个世代后，该种群中a基因的基因频率将会 （增大、减小），这种基因频率的改变是通过 实现的。
Ⅱ、果蝇的自然群体中，第Ⅱ号染色体的变异很多。下表表示为果蝇的三种第Ⅱ号染色体突变类型（A、B、C），在不同温度下的存活能力与标准型果蝇的比较（以标准型为100）。请分析并回答下面的问题。
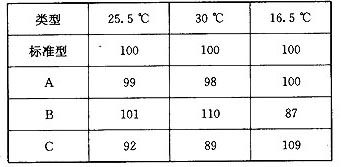
（1）分析表中数据并结合所学知识，可看出生物突变的特点是 ，因其具有上述特点，所以它不能决定生物进化的方向，那么生物进化的方向由 决定，提供进化原材料的是 。
（2）如果果蝇生存环境的温度明显下降，经过较长时间后，形成了一个新品种，将类似于 。如果这一新品种与原类型形成 ，就是一个新物种了。
