题目内容
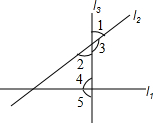如图，已知直线l1、l2、l3两两相交，且∠1=60°，∠2=
∠4，则∠3=________，∠5=________．
120° 90°
分析：根据邻补角的和等于180°列式计算即可求出∠3的度数；
先根据对顶角相等求出∠2的度数，再求出∠4，然后根据邻补角的和等于180°列式计算即可求出∠5的度数．
解答：∵∠1=60°，
∴∠3=180°-60°=120°；
∠2=∠1=60°，
∵∠2=∠4，
∴∠4=
∠2=×60°=90°，
∴∠5=180°-∠4=180°-90°=90°．
故答案为：120°，90°．
点评：本题考查了对顶角相等，邻补角互补的性质，仔细观察图形找出各角的关系是解题的关键．
分析：根据邻补角的和等于180°列式计算即可求出∠3的度数；
先根据对顶角相等求出∠2的度数，再求出∠4，然后根据邻补角的和等于180°列式计算即可求出∠5的度数．
解答：∵∠1=60°，
∴∠3=180°-60°=120°；
∠2=∠1=60°，
∵∠2=
∠4，∴∠4=
∠2=×60°=90°，∴∠5=180°-∠4=180°-90°=90°．
故答案为：120°，90°．
点评：本题考查了对顶角相等，邻补角互补的性质，仔细观察图形找出各角的关系是解题的关键．
练习册系列答案
相关题目
6、如图，已知直线l1，l2，l3相交于点O，∠1=35°，∠2=25°，则∠3等于（ ）
（2012•郯城县一模）如图，已知直线l1∥l2∥l3∥l4，相邻两条平行直线间的距离都是1，如果正方形ABCD的四个顶点分别在四条直线上，则cosα=（ ）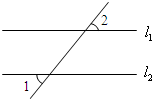
（2007•黔南州）如图，已知直线l1∥l2，∠1=50°，那么∠2=
如图：已知直线l1∥l2，且l3、l4和l1、l2分别交于点A、B和点C、D，点P在AB上，设∠ADP=∠1，∠DPC=∠2，∠BCP=∠3．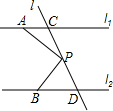
如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线l3上有点P（点P与点C、D不重合），点A在直线l1上，点B在直线l2上．