题目内容
14.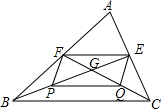 已知,如图,△ABC的中线BE,CF相交于点G,P,Q分别是BG,CG的中点.求证:
已知,如图,△ABC的中线BE,CF相交于点G,P,Q分别是BG,CG的中点.求证:(1)四边形EFPQ是平行四边形;
(2)BG=2GE,CG=2GF.
分析 (1)证明EF是△ABC的中位线,PQ是△BCG的中位线,由三角形中位线定理即可得出EF∥PQ,EF=PQ,即可得出结论;
(2)由平行四边形的性质得出对角线互相平分GE=GP,GF=GQ,即可得出结论.
解答 证明:(1)∵BE,CF是△ABC的中线,
∴EF是△ABC的中位线,
∴EF∥BC且EF=$\frac{1}{2}$BC,
∵P,Q分别是BG,CG的中点,
∴PQ是△BCG的中位线,BG=2GP,CG=2GQ,
∴PQ∥BC且PQ=$\frac{1}{2}$BC,
∴EF∥PQ且EF=PQ,
∴四边形EFPQ是平行四边形.
(2)由(1)得:四边形EFPQ是平行四边形,
∴GE=GP,GF=GQ,
∵BG=2GP,CG=2GQ,
∴BG=2GE,CG=2GF.
点评 本题考查了平行四边形的判定与性质、三角形的中位线定理;熟练掌握平行四边形的判定与性质,证明三角形中位线是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.用一个平面去截一个几何体,如果截面的形状是长方形,则这个几何体不可能是( )
| A. | 圆柱 | B. | 正方体 | C. | 圆锥 | D. | 五棱柱 |