题目内容
如图,等腰三角形ABC的顶角为120°,底边BC= ,则腰长AB为( )
,则腰长AB为( )
A.

B.

C.

D.

【答案】分析:过点A作AD⊥BC于点D,利用等腰三角形的性质,点D是BC的中点,故在△ABD中,可以求出AB的值.
解答: 解:过点A作AD⊥BC于点D,
解:过点A作AD⊥BC于点D,
∴BD=CD,∠BAD=∠CAD,
∴BD= ,
,
∵∠BAC=120°,
∴∠BAD=∠CAD=60°,
∴∠B=30°,
∴在Rt△ABD中,设AD=x,
则AB=2x,
根据勾股定理,x2+( )2=(2x)2,
)2=(2x)2,
解得,x= ,
,
所以AB=2× =
= .
.
故选C.
点评:本题主要考查了等腰三角形三线合一这一性质,即等腰三角形底边上的高线、中线,顶角的平分线三线合一.正确作出辅助线是解答本题的关键.
解答:
 解:过点A作AD⊥BC于点D,
解:过点A作AD⊥BC于点D,∴BD=CD,∠BAD=∠CAD,
∴BD=
 ,
,∵∠BAC=120°,
∴∠BAD=∠CAD=60°,
∴∠B=30°,
∴在Rt△ABD中,设AD=x,
则AB=2x,
根据勾股定理,x2+(
 )2=(2x)2,
)2=(2x)2,解得,x=
 ,
,所以AB=2×
 =
= .
.故选C.
点评:本题主要考查了等腰三角形三线合一这一性质,即等腰三角形底边上的高线、中线,顶角的平分线三线合一.正确作出辅助线是解答本题的关键.

练习册系列答案
相关题目
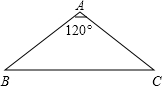 如图,等腰三角形ABC的顶角为120°,底边BC=
如图,等腰三角形ABC的顶角为120°,底边BC=
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
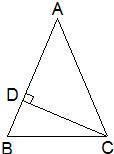 9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( )
9、如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于( ) (1)他们的说法合理吗?为什么?
(1)他们的说法合理吗?为什么?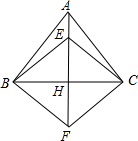 如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,
如图,等腰三角形ABC中,AB=AC,AH垂直BC,点E是AH上一点,延长AH至点F,使FH=EH,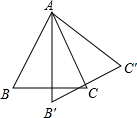 如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转
如图,等腰三角形ABC(AB=AC)的底角为50°,绕点A逆时针旋转一定角度后得△AB′C′,那么△AB′C′绕点A旋转