题目内容
 (2012•梁子湖区模拟)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于N,且S△ABC=24,那么S四边形ANME-S△DMN=
(2012•梁子湖区模拟)如图,DE是△ABC的中位线,M是DE的中点,CM的延长线交AB于N,且S△ABC=24,那么S四边形ANME-S△DMN=4
4
.分析:连接AM,由于DE是△ABC的中位线,由三角形中位线定理得出DE∥BC,且DE=
BC.由M是DE中点,可知DM=
BC,在△BCN中,利用平行线分线段成比例定理,可得DN=
BD,即DN=
AD,于是S△DMN=
S△ADM,而S△ADM=
S△ADE=
S△ABC=3,那么S四边形ANME也可求,两者面积之差也就可求.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 8 |
解答: 解:∵DE是△ABC的中位线,
解:∵DE是△ABC的中位线,
∴DE∥BC,DE=
BC,
∴△ADE∽△ABC,
∴S△ADE=
S△ABC=6.
连接AM.
∵M是DE的中点,
∴S△ADM=
S△ADE=3.
∵DE∥BC,DM=
BC,
∴DN=
BN,
∴DN=
BD=
AD.
∴S△DNM=
S△ADM=1,
∴S四边形ANME=S△ADE-S△DNM=6-1=5,
∴S四边形ANME-S△DMN=5-1=4.
故答案为4.
 解:∵DE是△ABC的中位线,
解:∵DE是△ABC的中位线,∴DE∥BC,DE=
| 1 |
| 2 |
∴△ADE∽△ABC,
∴S△ADE=
| 1 |
| 4 |
连接AM.
∵M是DE的中点,
∴S△ADM=
| 1 |
| 2 |
∵DE∥BC,DM=
| 1 |
| 4 |
∴DN=
| 1 |
| 4 |
∴DN=
| 1 |
| 3 |
| 1 |
| 3 |
∴S△DNM=
| 1 |
| 3 |
∴S四边形ANME=S△ADE-S△DNM=6-1=5,
∴S四边形ANME-S△DMN=5-1=4.
故答案为4.
点评:本题主要考查了三角形的中位线定理,相似三角形的判定与性质,平行线分线段成比例定理,综合性较强,难度中等.利用平行线分线段成比例定理,得出DN=
BD,即DN=
AD是解题的关键.
| 1 |
| 3 |
| 1 |
| 3 |

练习册系列答案
相关题目
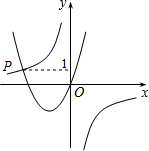 (2012•梁子湖区模拟)如图,已知函数
(2012•梁子湖区模拟)如图,已知函数 (2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )
(2012•梁子湖区模拟)如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积,关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为( )