题目内容
 26、如图所示,每个小正方形的边长为1个单位长度
26、如图所示,每个小正方形的边长为1个单位长度(1)写出A、B、C的坐标;
(2)作△ABC关于y轴对称的△A1B1C1,写出A1,B1,C1的坐标;
(3)作△A1B1C1关于x轴对称的△A2B2C2,写出A2、B2、C2的坐标.写出△ABC与△A2B2C2满足什么变换关系.
分析:(1)根据平面直角坐标系写出即可;
(2)先找出出A、B、C关于y轴的的对应的对称点A1,B1,C1的位置,然后顺次连接即可;
(3)找出A1,B1,C1关于x轴的对应的对称点A2、B2、C2的位置,然后顺次连接即可;根据点的坐标的变化特点即可判断.
(2)先找出出A、B、C关于y轴的的对应的对称点A1,B1,C1的位置,然后顺次连接即可;
(3)找出A1,B1,C1关于x轴的对应的对称点A2、B2、C2的位置,然后顺次连接即可;根据点的坐标的变化特点即可判断.
解答: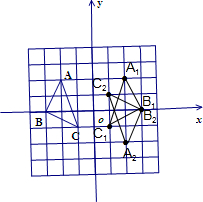 解:(1)A、B、C的坐标分别为:
解:(1)A、B、C的坐标分别为:
A(-2,2),B(-3,0),C(-1,-1);
(2)图形如右,
A1,B1,C1的坐标分别为:A1(2,2),B1(3,0),C1(1,-1);
(3)图形如右,
A2,B2,C2的坐标分别为:A2(2,-2),B2(3,0),C2(1,1);
∵点ABC的坐标与点A2,B2,C2的坐标横坐标与纵坐标都互为相反数,
∴它们关于原点对称,
∴△ABC与△A2B2C2满足关于原点中心对称.
 解:(1)A、B、C的坐标分别为:
解:(1)A、B、C的坐标分别为:A(-2,2),B(-3,0),C(-1,-1);
(2)图形如右,
A1,B1,C1的坐标分别为:A1(2,2),B1(3,0),C1(1,-1);
(3)图形如右,
A2,B2,C2的坐标分别为:A2(2,-2),B2(3,0),C2(1,1);
∵点ABC的坐标与点A2,B2,C2的坐标横坐标与纵坐标都互为相反数,
∴它们关于原点对称,
∴△ABC与△A2B2C2满足关于原点中心对称.
点评:本题考查了利用轴对称变换作图,找出对称后的对应点的位置是作图的关键,难度不大,需要仔细找点的位置.

练习册系列答案
相关题目
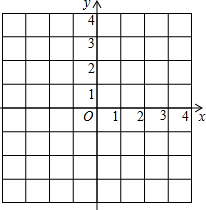 如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现: 如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现:
如图,平面直角坐标系中的方格阵表示一个纵横交错的街道模型的一部分,以O为原点,建立如图所示的平面直角坐标系,x轴,y轴的正方向分别表示正东、正北方向,出租车只能沿街道(网格线)行驶,且从一个路口(格点)到另一个路口,必须选择最短路线,称最短路线的长度为两个街区之间的“出租车距离”.设图中每个小正方形方格的边长为1个单位.可以发现: