题目内容
【题目】如图，抛物线
与x轴交于A（﹣2，0）、B（6，0）两点．
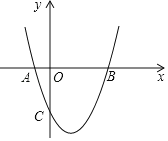
（1）求该抛物线的解析式；
（2）点P为y轴左侧抛物线上一个动点，若S△PAB=32，求此时P点的坐标．
【答案】（1）
;（2）
或
【解析】
（1）将A、B两点的坐标代入即可求出抛物线的解析式；
（2）过点P作PE⊥x轴，然后利用S△PAB求出PE的长即可得到P点纵坐标有两种情况，分别求出横坐标，再根据点P为y轴左侧抛物线上即可排除.
解：（1）将A、B两点的坐标代入得：
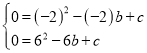
解得：
∴该抛物线的解析式为：.
（2）过点P作PE⊥x轴，
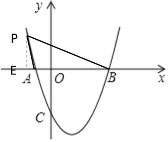
∵A（﹣2，0）、B（6，0）
∴AB=6－（﹣2）=8
∵S△PAB=32，
∴S△PAB=
=32
解得：PE=8
∴P点纵坐标为±8
当P点纵坐标为﹣8时，代入到解析式中，得：
解得：
（不符合点P在y轴左侧，舍去）
此时P点坐标为：；
当P点纵坐标为8时，代入到解析式中，得：
解得：
（不符合点P在y轴左侧，舍去）
此时P点坐标为：
综上所述：P点坐标为：或.
练习册系列答案
名校课堂系列答案
相关题目
