Question

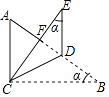
【题目】如图，AD是△ABC的中线，tanB=，cosC=，AC=．求：

（1）BC的长；
（2）sin∠ADC的值．

Answer 1

【答案】
（1）

解：过点A作AE⊥BC于点E，

∵cosC=，

∴∠C=45°，

在Rt△ACE中，CE=ACcosC=1，

∴AE=CE=1，

在Rt△ABE中，tanB=，即=，

∴BE=3AE=3，

∴BC=BE+CE=4；

（2）

解：∵AD是△ABC的中线，

∴CD=BC=2，

∴DE=CD﹣CE=1，

∵AE⊥BC，DE=AE，

∴∠ADC=45°，

∴sin∠ADC=．

【解析】（1）过点A作AE⊥BC于点E，根据cosC=，求出∠C=45°，求出AE=CE=1，根据tanB=，求出BE的长即可；
（2）根据AD是△ABC的中线，求出BD的长，得到DE的长，得到答案．