题目内容
要使(ax2-3x)(x2-2x-1)的展开式中不含x3项,则a=分析:先展开式子,找出所有x3项的系数,令其为0,即可求a的值.
解答:解:∵(ax2-3x)(x2-2x-1),
=ax4-2ax3-ax2-3x3+6x2+3x,
=ax4-(2a+3)x3-(a-6)x2+3x,
又∵展开式中不含x3项
∴2a+3=0,
解得a=-
.
=ax4-2ax3-ax2-3x3+6x2+3x,
=ax4-(2a+3)x3-(a-6)x2+3x,
又∵展开式中不含x3项
∴2a+3=0,
解得a=-
| 3 |
| 2 |
点评:本题主要考查了多项式乘多项式的运算,注意当要求多项式中不含有哪一项时,应让这一项的系数为0,注意各项符号的处理.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
要使关于x的方程ax2+3x+4=0有两个不相等的实数根,则a的取值是( )
A、a<
| ||
B、a≤
| ||
C、a<
| ||
D、a>
|
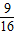
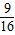 且a≠0
且a≠0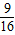 且a≠0
且a≠0