题目内容
 如图,AD、CE均是△ABC的高,交于H.若EB=EH=3,AE=4,则CH的长为________.
如图,AD、CE均是△ABC的高,交于H.若EB=EH=3,AE=4,则CH的长为________.
1
分析:由∠BAD+∠B=90°,∠BCE+∠B=90°得到∠BAD=∠BCE,进而得到△HAE∽△BCE,又得到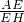 =
= ,EC=
,EC= •3=4∴CH=EC-EH=4-3=1而解得.
•3=4∴CH=EC-EH=4-3=1而解得.
解答:∵∠BAD+∠B=90°;∠BCE+∠B=90°;
∴∠BAD=∠BCE
∴△HAE∽△BCE∴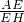 =
= ,
,
∴EC= •3=4
•3=4
∴CH=EC-EH=4-3=1.
点评:本题考查了勾股定理,本题先确定直角三角形,利用勾股定理来计算.
分析:由∠BAD+∠B=90°,∠BCE+∠B=90°得到∠BAD=∠BCE,进而得到△HAE∽△BCE,又得到
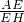 =
= ,EC=
,EC= •3=4∴CH=EC-EH=4-3=1而解得.
•3=4∴CH=EC-EH=4-3=1而解得.解答:∵∠BAD+∠B=90°;∠BCE+∠B=90°;
∴∠BAD=∠BCE
∴△HAE∽△BCE∴
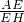 =
= ,
,∴EC=
 •3=4
•3=4∴CH=EC-EH=4-3=1.
点评:本题考查了勾股定理,本题先确定直角三角形,利用勾股定理来计算.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,AD、CE均是△ABC的高,交于H.若EB=EH=3,AE=4,则CH的长为
如图,AD、CE均是△ABC的高,交于H.若EB=EH=3,AE=4,则CH的长为 如图,AD、CE均是△ABC的高,交于H,且AE=CE,若AB=17,CH=7,则AH的长为
如图,AD、CE均是△ABC的高,交于H,且AE=CE,若AB=17,CH=7,则AH的长为
