题目内容
14.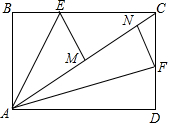 如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是9+2$\sqrt{6}$.
如图,矩形ABCD,将它分别沿AE和AF折叠,恰好使点B,C落到对角线AC上点M,N处,已知MN=2,NC=1,则矩形ABCD的面积是9+2$\sqrt{6}$.
分析 由折叠的性质得,AB=AM,AN=AD,设AB=x,则AD=x+2,AC=x+3,根据勾股定理列方程即可得到结论.
解答 解:由折叠的性质得,AB=AM,AN=AD,
∴AD-AB=AN-AM=MN=2,
设AB=x,则AD=x+2,AC=x+3,
∵四边形ABCD是矩形,
∴∠D=90°,CD=AB,
∴AD2+CD2=AC2,即(x+2)2+x2=(x+3)2,
∴x=1+$\sqrt{6}$(负值舍去),
∴AB=1+$\sqrt{6}$,AD=3+$\sqrt{6}$,
∴S矩形ABCD=(1+$\sqrt{6}$)(3+$\sqrt{6}$)=9+4$\sqrt{6}$;
故答案为:9+4$\sqrt{6}$.
点评 本题主要考查了折叠的性质、矩形的性质、勾股定理等,综合运用各定理是解答此题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
5.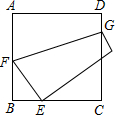 如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为( )
如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为( )
 如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为( )
如图,将正方形ABCD的一角折向边CD,使点A与CB上一点E重合,若BE=1,CE=2,则折痕FG的长度为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 4 |
9.下列各组数据中,平均数和中位数相等的是( )
| A. | 1,2,3,4,5 | B. | 1,3,4,5,6 | C. | 1,2,4,5,6 | D. | 1,2,3,5,6 |
3.一个不透明的布袋里装有6个黑球和3个白球,它们除颜色外其余都相同,从中任意摸出一个球,是白球的概率为( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 如图是由若干个正方体组成的几何体的俯视图,数字表示该位置上小正方体的个数,则该几何体左视图可能是( )
如图是由若干个正方体组成的几何体的俯视图,数字表示该位置上小正方体的个数,则该几何体左视图可能是( )



 如图,四个完全相同的小球上分别写有:0,$\frac{2}{3}$,-5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为$\frac{1}{4}$.
如图,四个完全相同的小球上分别写有:0,$\frac{2}{3}$,-5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为$\frac{1}{4}$. 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.
如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=-2x-1经过抛物线上一点B(-2,m),且与y轴、直线x=2分别交于点D、E.