题目内容
【题目】有![]() 、
、![]() 、
、![]() 三家工厂依次坐落在一条笔直的公路边,甲、乙两辆运货卡车分别从
三家工厂依次坐落在一条笔直的公路边,甲、乙两辆运货卡车分别从![]() 、
、![]() 工厂同时出发,沿公路匀速驶向
工厂同时出发,沿公路匀速驶向![]() 工厂,最终到达
工厂,最终到达![]() 工厂,设甲、乙两辆卡车行驶
工厂,设甲、乙两辆卡车行驶![]() 后,与
后,与![]() 工厂的距离分别为
工厂的距离分别为![]() 、
、![]() (
(![]() ).
).![]() 、
、![]() 与
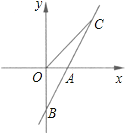
与![]() 函数关系如图所示,根据图象解答下列问题.(提示:图中较粗的折线表示的是
函数关系如图所示,根据图象解答下列问题.(提示:图中较粗的折线表示的是![]() 与
与![]() 的函数关系.)
的函数关系.)
(![]() )
)![]() 、
、![]() 两家工厂之间的距离为__________
两家工厂之间的距离为__________ ![]() ,
, ![]() __________,
__________, ![]() 点坐标是__________.
点坐标是__________.
(![]() )求甲、乙两车之间的距离不超过
)求甲、乙两车之间的距离不超过![]() 时,
时, ![]() 的取值范围.
的取值范围.

【答案】(1)见解析;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)根据y轴的最大距离为B、C两地间的距离,再加上A、B两地间的距离即可;先求出甲的速度,再求出到达C地的时间,然后加上0.5即为a的值;利用待定系数法求一次函数解析式求出甲从B地到C地的函数解析式,再求出乙的解析式,然后联立求解即可得到点P的坐标;
(2)根据两函数解析式列出不等式组求解即可.
试题解析:解:(1)由图可知,A、B两地相距30km,B、C两地相距90km,所以,A、C两家工厂之间的距离为30+90=120km,甲的速度为:30÷0.5=60km/h,90÷60=1.5小时,∴a=0.5+1.5=2;
设甲:0.5≤x≤2时的函数解析式为y=kx+b,∵函数图象经过点(0.5,0)、(2,90),∴![]() ,解得:
,解得: ![]() ,∴y=60x﹣30,乙的速度为90÷3=30km/h,乙函数解析式为:y=30x,联立
,∴y=60x﹣30,乙的速度为90÷3=30km/h,乙函数解析式为:y=30x,联立![]() ,解得:
,解得: ![]() ,所以,点P(1,30);
,所以,点P(1,30);
故答案为:120,2,(1,30);
(2)∵甲、乙两车之间的距离不超过10km,∴ ![]() ,解不等式①得,x≥
,解不等式①得,x≥![]() ,解不等式②得,x≤
,解不等式②得,x≤![]() ,所以,x的取值范围是
,所以,x的取值范围是![]() ≤x≤
≤x≤![]() ;
;
当甲车停止后,乙行驶![]() 小时时,两车相距10km,故
小时时,两车相距10km,故![]() ≤x≤3时,甲、乙两车之间的距离不超过10km.
≤x≤3时,甲、乙两车之间的距离不超过10km.
综上所述:x的取值范围是![]() ≤x≤
≤x≤![]() 或
或![]() ≤x≤3甲、乙两车之间的距离不超过10km.
≤x≤3甲、乙两车之间的距离不超过10km.