题目内容
如图1,直角梯形ABCD中,∠A=∠B=90°,AD=AB=6cm,BC=8cm,点E从点A出发沿AD方向以1cm/s的速度向终点D运动;点F从点C出发沿CA方向以2cm/s的速度向终点A运动,当点E、点F中有一点运动到终点,另一点也随之停止.设运动时间为ts.
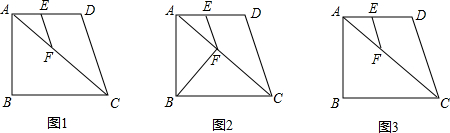
(1)当t为何值时,△AEF和△ACD相似?
(2)如图2,连接BF,随着点E、F的运动,四边形ABFE可能是直角梯形?若可能,请求出t的值及四边形ABFE的面积;若不能,请说明理由;
(3)当t为何值时,△AFE的面积最大?最大值是多少?
解:(1)当运动t秒时,△AEF∽△ADC时,
∴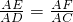 ,AE=t,CF=2t,
,AE=t,CF=2t,
∴AF=AC-2t
∵∠A=∠B=90°,AD=AB=6cm,BC=8cm,由勾股定理,得
AC=10cm,
∴AF=10-2t
∴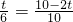 ,解得
,解得
t=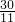
当运动t秒时,△AEF∽△ACD时,
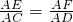
∴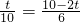 解得:
解得:
t=
(2)设t秒后四边形AEFB是直角梯形,延长EF交BC于点G,

∴EG⊥AD,EG⊥BC
∵∠B=90°,
∴AB⊥BC,
∴EG∥AB,且AD∥BC
∴△CGF∽△CBA,四边形AEGB为矩形
∴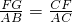 ,EG=AB=6
,EG=AB=6
∴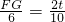 ,
,
∴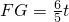
∴EF=6-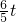 ,
,
在Rt△AEF中,由勾股定理,得
t2+(6- t)2=(10-2t)2,解得
t)2=(10-2t)2,解得
t1=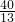 ,t2=
,t2= (不符合题意应舍去)
(不符合题意应舍去)
∴EF=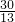 ,AE=
,AE=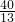
∴S四边形ABFE=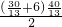
=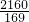 cm2
cm2
(3)过点F作MN⊥AD于M,交BC于点N
∴∠DEG=90°.
∵AD∥BC,
∴∠BGE=∠DEG=90°.
∵∠B=90°,
∴EG∥AB,
∴△CFN∽△CAB,
∴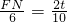
∴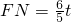 ,
,
∴MF=6-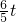 ,
,
∴S△AFE=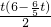
=- (t-
(t- )2+
)2+ .
.
∴当t= 时,S△AFE最大,最大值是
时,S△AFE最大,最大值是 .
.
分析:(1)E、F在移动的过程中,△AEF和△ACD相似有两种情况,△AEF∽△ACD和△AEF∽△ADC,根据相似三角形的性质就可以求出t的值.
(2)E、F移动t秒后ABFE是直角梯形,则FE⊥AD,延长EF交BC于点G,同样利用三角形相似把FG表示出来,从而求出EF,根据勾股定理建立等量关系求出t值,就可以求出梯形的面积.
(3)过点F作MN⊥AD于M,交BC于点N,可以证明△CFN∽△CAB,表示出FN,从而表示出FM,利用三角形的面积公式及uky表示出三角形的面积S与t的函数关系式,从而求其解.
点评:本题是一道有关直角梯形的结合解答题,考查了二次函数的最值,相似三角形的判定与性质,勾股定理的运用.
∴
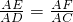 ,AE=t,CF=2t,
,AE=t,CF=2t,∴AF=AC-2t
∵∠A=∠B=90°,AD=AB=6cm,BC=8cm,由勾股定理,得
AC=10cm,
∴AF=10-2t
∴
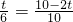 ,解得
,解得t=
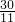
当运动t秒时,△AEF∽△ACD时,
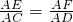
∴
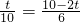 解得:
解得:t=

(2)设t秒后四边形AEFB是直角梯形,延长EF交BC于点G,

∴EG⊥AD,EG⊥BC
∵∠B=90°,
∴AB⊥BC,
∴EG∥AB,且AD∥BC
∴△CGF∽△CBA,四边形AEGB为矩形
∴
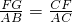 ,EG=AB=6
,EG=AB=6∴
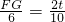 ,
,∴
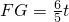
∴EF=6-
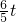 ,
,在Rt△AEF中,由勾股定理,得
t2+(6-
 t)2=(10-2t)2,解得
t)2=(10-2t)2,解得t1=
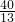 ,t2=
,t2= (不符合题意应舍去)
(不符合题意应舍去)∴EF=
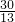 ,AE=
,AE=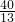
∴S四边形ABFE=
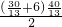
=
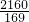 cm2
cm2(3)过点F作MN⊥AD于M,交BC于点N
∴∠DEG=90°.
∵AD∥BC,
∴∠BGE=∠DEG=90°.
∵∠B=90°,
∴EG∥AB,
∴△CFN∽△CAB,
∴
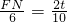
∴
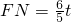 ,
,∴MF=6-
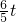 ,
,∴S△AFE=
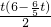
=-
 (t-
(t- )2+
)2+ .
.∴当t=
 时,S△AFE最大,最大值是
时,S△AFE最大,最大值是 .
.分析:(1)E、F在移动的过程中,△AEF和△ACD相似有两种情况,△AEF∽△ACD和△AEF∽△ADC,根据相似三角形的性质就可以求出t的值.
(2)E、F移动t秒后ABFE是直角梯形,则FE⊥AD,延长EF交BC于点G,同样利用三角形相似把FG表示出来,从而求出EF,根据勾股定理建立等量关系求出t值,就可以求出梯形的面积.
(3)过点F作MN⊥AD于M,交BC于点N,可以证明△CFN∽△CAB,表示出FN,从而表示出FM,利用三角形的面积公式及uky表示出三角形的面积S与t的函数关系式,从而求其解.
点评:本题是一道有关直角梯形的结合解答题,考查了二次函数的最值,相似三角形的判定与性质,勾股定理的运用.

练习册系列答案
相关题目
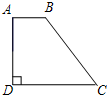 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
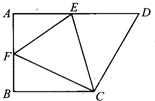 12、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,将直角梯形ABCD沿CE折叠,使点D落在AB上的F点,若AB=BC=12,EF=10,∠FCD=90°,则AF=
12、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,将直角梯形ABCD沿CE折叠,使点D落在AB上的F点,若AB=BC=12,EF=10,∠FCD=90°,则AF=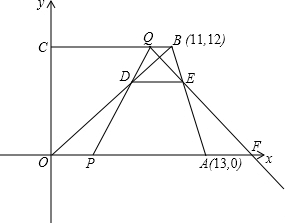 为t(单位:秒).
为t(单位:秒). (2013•黑龙江)如图,在直角梯形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的个数是( )
(2013•黑龙江)如图,在直角梯形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的个数是( ) 如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=a,BC=b,AB=c,以AB为直径作⊙O.试探究:
如图,在直角梯形ABCD中,AD∥BC,∠D=90°,AD=a,BC=b,AB=c,以AB为直径作⊙O.试探究: