题目内容
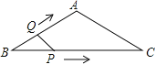
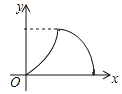
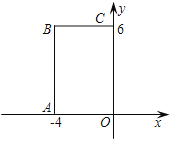
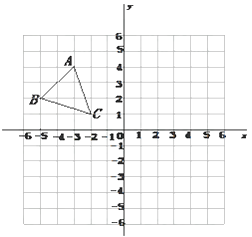
【题目】如图,在平面直角坐标系中,![]() 是坐标原点,抛物线
是坐标原点,抛物线![]() 经过
经过![]() ,
,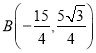 两点,连接
两点,连接![]() ,
,![]() .
.
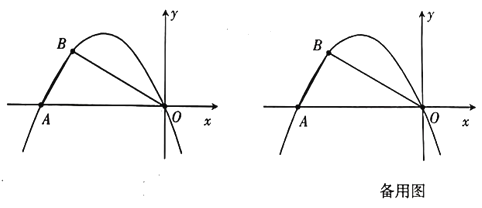
(1)求抛物线表达式;
(2)点![]() 是第三象限内的一个动点,若
是第三象限内的一个动点,若![]() 与
与![]() 全等,请直接写出点
全等,请直接写出点![]() 坐标______;
坐标______;
(3)若点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 作匀速运动,速度为每秒1个单位长度,同时线段
作匀速运动,速度为每秒1个单位长度,同时线段![]() 上另一个点
上另一个点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 作匀速运动,速度为每秒2个单位长度(当点
作匀速运动,速度为每秒2个单位长度(当点![]() 到达点
到达点![]() 时,点
时,点![]() 也同时停止运动).过点
也同时停止运动).过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,以
,以![]() 为边,在
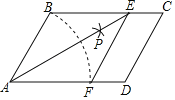
为边,在![]() 左侧作等边三角形
左侧作等边三角形![]() (当点
(当点![]() 运动时,点
运动时,点![]() 、点
、点![]() 也随之运动).过点
也随之运动).过点![]() 作
作![]() 轴的垂线,与直线
轴的垂线,与直线![]() 交于点
交于点![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,以
,以![]() 为边,在
为边,在![]() 的右侧作等边三角形
的右侧作等边三角形![]() (当点
(当点![]() 运动时,点
运动时,点![]() 、点
、点![]() 也随之运动).当点
也随之运动).当点![]() 运动
运动![]() 秒时,
秒时,![]() 有一条边所在直线恰好过
有一条边所在直线恰好过![]() 的重心,直接写出此刻
的重心,直接写出此刻![]() 的值____________.
的值____________.
【答案】(1)![]() ;(2)
;(2) 或
或 ;(3)
;(3)![]() 或
或![]()
【解析】
(1)将A、B两点坐标代入解析式,可求得;
(2)存在2种情况,一种是△AOB≌△AOC,则点B与点C关于x轴对称,可求得C点坐标;另一种是△AOB≌△OAC,则OC∥AB,AC∥BO,联立直线AC和OC的解析式,可求得点C的坐标;
(3)有2大类情况,一种是点D在点H的左侧,还有一种是点D在点H的右侧,画图可得出只有点D在点H的左侧有可能.又分为3种情况,一种是DF过△HMN的重心,第二种是GF过△HMN的重心,第三种是GD过△HMN的重心.
(1)∵抛物线过点A(-5,0),B(![]() ,
,![]() )
)
∴![]() ,
,![]()
解得:![]() ,
,![]()
∴抛物线解析式为:![]() ;
;
(2)情况一:△AOB≌△AOC,图形如下
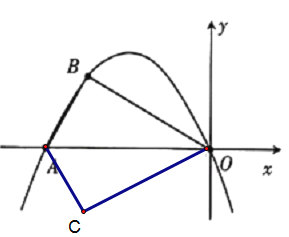
从图形易知,点C与点B关于x轴对称
∵B(![]() ,
,![]() ),∴C(
),∴C(![]() ,
,![]() );
);
情况二:△AOB≌△OBC,图形如下
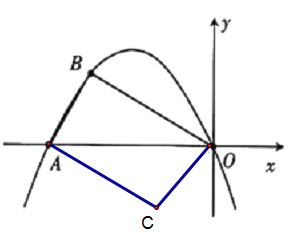
∴∠BAO=∠AOC,∠BOA=∠CAO
∴AB∥CO,BO∥AC
∵A(-5,0),B(![]() ,
,![]() )
)
∴直线AB的解析式为:y=![]()
直线OB的解析式为:y=![]()
∴OC的解析式为:y=![]()
AC的解析式设为:y=![]() ,将点A代入得:y=
,将点A代入得:y=![]()
联立OC和AC的解析,解得:x=![]() ,y=
,y=![]()
∴C(![]() ,
,![]() );
);
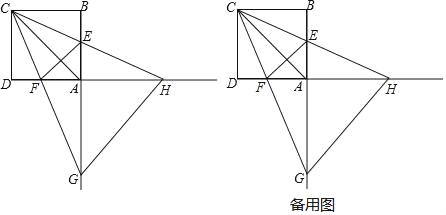
(3)当点D在点H的左侧时,即5>3t,t<![]() 时,图形如下
时,图形如下

根据题意可知
D(-t,0),H(2t-5,0)
∵OB的解析式为:y=![]()
∴E(-t,![]() ),F(-t,
),F(-t,![]() ),L(2t-5,
),L(2t-5,![]() ),M(2t-5,
),M(2t-5,![]() )
)
∴MH=![]() ,HD=5-3t,FD=
,HD=5-3t,FD=![]()
∵△GFD是等边三角形,∴易知FD∥MH,FG∥HN,GD∥MN
情况一:当DF过△MHN的重心时,图形如下,连接LN,交FD于点O

则点O为△MHN的重心
∴ON:OL=2:1,∴OL=![]()
∵△HMN是等边三角形
∴NL=![]() MH=5
MH=5![]() t
t
∵OL=HD=5-3t
∴5-3t=![]()
解得:t=![]() (成立);
(成立);
情况二:FG过△HMN的重心,如下图,GF交HM于点P,过点P作FD的垂线,交FD于点Q,过点M作HN的垂线,交GF于点O,交HN于点R

则点O为△HNM的中线,∴MO:OR=2:1
易知△MOP∽△MRH,∴MP:PH=2:1
∴PH=![]()
由题意可知,PQ=HD=5-3t,∠FPQ=30°
∴在Rt△FPQ中,FQ=![]()
∴QD=FD-FQ=![]()
∴PH=QD=![]()
∴![]()
解得:t=![]() (成立);
(成立);
情况三:DG过△MHN的重心,如下图,HN与GD交于点S,过点S作x轴的垂线,交x轴于点T
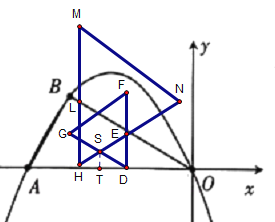
易知∠SDH=∠SHD=30°,∠HSD=120°,HD=5-3t
则在Rt△SHR中,HT=![]() ,ST=
,ST=![]() ,SH=
,SH=![]()
同理:SH=![]()
∴![]()
t=-5(舍)
综上得:t=![]() 或t=
或t=![]() .
.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
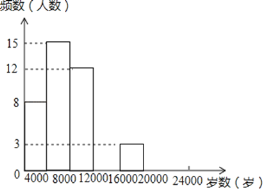
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37600名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师恰好不在同一组的概率.