题目内容
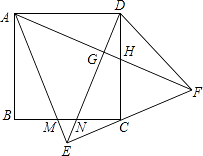
【题目】如图,在四边形![]() 中,已知
中,已知![]() ,
,![]() ,且
,且![]() .
.

(1)填空:![]() _____,
_____,![]() ______,
______,![]() _______;
_______;
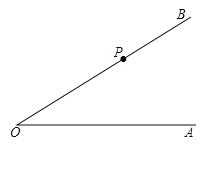
(2)点![]() 为射线
为射线![]() 上一任意一点,连接
上一任意一点,连接![]() ,作
,作![]() 的平分线
的平分线![]() ,交射线
,交射线![]() 于点
于点![]() ,作
,作![]() 的平分线
的平分线![]() ,交直线
,交直线![]() 于点
于点![]() ,请探究射线
,请探究射线![]() 与
与![]() 之间的位置关系,并加以证明;
之间的位置关系,并加以证明;
(3)连接![]() ,若
,若![]() 恰好平分
恰好平分![]() ,则在(2)问的条件下,是否存在角度
,则在(2)问的条件下,是否存在角度![]() ,使得当
,使得当![]() 时,有
时,有![]() (其中
(其中![]() 为不超过10的正整数)?若存在,求出
为不超过10的正整数)?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;
;![]() ;
;![]() (2)
(2)![]() ;证明见详解(3)存在;
;证明见详解(3)存在;![]() 、
、![]() 或
或![]()
【解析】
(1)根据垂直的定义、平行线的性质、四边形的内角和即可得解;
(2)按照题目要求画出图形后,根据已知条件、角平分线的性质、平行线的性质和判定即可得到结论并证明;
(3)结合图形根据平行线的性质、角平分线的性质、角的和差可列出![]() ,再由
,再由![]() 、
、![]() 的取值范围即可求得结论.
的取值范围即可求得结论.
解:(1)∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]() ;
;
(2)按照题目要求作图:
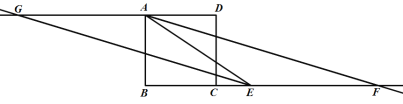
猜想:射线![]() 与
与![]() 的位置关系是:
的位置关系是:![]()
证明: ∵![]() 平分
平分![]() ,
,![]() 平分
平分![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]() ;
;
(3)在(2)问的条件下,连接![]() ,如图:
,如图:
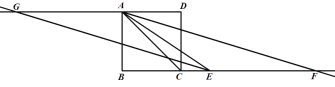
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]() 恰好平分
恰好平分![]() ,由(1)可知
,由(1)可知![]()
∴![]()
∵![]() 为射线
为射线![]() 上一任意一点
上一任意一点
∴![]()
∵![]() 为不超过10的正整数
为不超过10的正整数
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
∴存在角度![]() ,使得当
,使得当![]() 时,有
时,有![]() (其中
(其中![]() 为不超过10的正整数);
为不超过10的正整数);![]() 、
、![]() 或
或![]() .
.

练习册系列答案
相关题目