题目内容
20.计算:(1)(-3a2b3)2•(-a3b2)5÷a2b4;
(2)($\frac{2}{3}$)2012×(-1.5)2013÷(-1)2014;
(3)[x(x2y2-xy)-y(x2-x3y)]÷3x2y;
(4)(5x+7y-3)(5x-7y+3);
(5)(a+2b-c)2;
(6)(x+2y)2(x-2y)2.
分析 (1)首先计算乘方,把除法转化为乘法,然后计算式子的乘法即可;
(2)逆用积的乘方法则即可求解;
(3)首先利用单项式与多项式的乘法法则计算括号内的式子、合并同类项,然后计算多项式与单项式的除法即可;
(4)利用平方差公式和完全平方公式即可求解;
(5)逆用积的乘法法则,然后利用平方差公式计算,最后利用完全平方公式即可求解.
解答 解:(1)原式=9a4b6•(-a15b10)•(a-2 b-4)=-9a17b12;
(2)原式=($\frac{2}{3}$)2012×(-$\frac{3}{2}$)2013=[$\frac{2}{3}$×(-$\frac{3}{2}$)]2012×(-$\frac{3}{2}$)=(-1)2012×(-$\frac{3}{2}$)=-$\frac{3}{2}$;
(3)原式=(x3y2-x2y-x2y+x3y2)÷3x2y
=(2x3y2-2x2y)÷3x2y
=$\frac{2}{3}$xy-$\frac{2}{3}$;
(4)原式=(5x)2-(7y-3)2=25x2-(49y2-42y+9)=25x2-49y2+42y-9;
(5)原式=(a+2b)2-2c(a+2b)+c2=a2+4ab+4b2-2ac-4bc+c2;
(6)原式=[(x+2y)(x-2y)]2=(x2-4y2)2=x4-8x2y2+16y4.
点评 本题考查了整式的混合运算,正确运用运算性质,以及乘法公式是关键.

练习册系列答案
相关题目
10.下列命题的逆命题是真命题的是( )
| A. | 同位角相等 | B. | 对顶角相等 | ||
| C. | 钝角三角形有两个锐角 | D. | 两直线平行,内错角相等 |
11.一元二次方程x2-4=0的根是( )
| A. | x=2 | B. | x=±2 | C. | x=4 | D. | x=±4 |
5.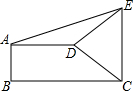 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( )
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( )
 如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( )
如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,∠BCD=45°,将腰CD以点D为中心逆时针旋转90°至ED,连结AE,CE,则△ADE的面积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.如果x是最大的负整数,y绝对值最小的整数,则-x2016+y的值是( )
| A. | -2000 | B. | -1 | C. | 1 | D. | 2016 |
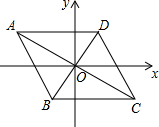 如图,已知点A的坐标为(-2$\sqrt{3}$,2),点B的坐标为(-1,-$\sqrt{3}$),菱形ABCD的对角线交于坐标原点O.
如图,已知点A的坐标为(-2$\sqrt{3}$,2),点B的坐标为(-1,-$\sqrt{3}$),菱形ABCD的对角线交于坐标原点O.