题目内容
设P是边长为1的正△ABC内任一点，L=PA+PB+PC，求证：
≤L＜2．
| 3 |
证明：（1）顺时针旋转△BPC60°，可得△PBE为等边三角形．
即得要使PA+PB+PC=AP+PE+EF′最小，只要AP，PE，EF′在一条直线上，
即如下图：可得最小L=
| 3 |
（2）过P点作BC的平行线交AB，AC于点D，F．
由于∠APD＞∠AFP=∠ADP，
推出AD＞AP ①
又∵BD+DP＞BP ②
和PF+FC＞PC ③
又∵DF=AF ④
由①②③④可得：最大L＜2；
由（1）和（2）即得：
| 3 |
练习册系列答案
名题金卷系列答案
相关题目
设P是边长为1的正△ABC内任一点，L=PA+PB+PC，求证：
设PQ是边长为1的正△ABC的外接圆内的一条弦．已知AB和AC的中点都在PQ上．那么，PQ的长等于________．
设P是边长为1的正△ABC内任一点，L=PA+PB+PC，求证：
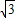≤L＜2．
≤L＜2．