题目内容
已知抛物线y=x2-2x-3，若点P（3，0）与点Q关于该抛物线的对称轴对称，则点Q的坐标是 ．
考点：二次函数图象上点的坐标特征
专题：
分析：根据抛物线解析式求出抛物线对称轴为x=1，再根据图象得出点p（-2，5）关于对称轴对称点Q的纵坐标不变，两点横坐标到对称轴的距离相等，都为3，得到Q点坐标为（4，5）．
解答：解：∵x=-
=-
=1．
∴P（3，0）关于对称轴的对称点Q的坐标是（-1，0）．
故点Q的坐标是（-1，0）．
故答案为（-1，0）．
| b |
| 2a |
| -2 |
| 2×1 |
∴P（3，0）关于对称轴的对称点Q的坐标是（-1，0）．
故点Q的坐标是（-1，0）．
故答案为（-1，0）．
点评：此题考查抛物线解析式与图象性质，以及轴对称点的相关性质，体现数形结合思想．
练习册系列答案
相关题目
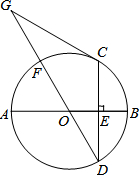如图，AB是⊙O的直径，CD是弦，CD⊥AB于点E，点G在直径DF的延长线上，∠D=∠G=30．
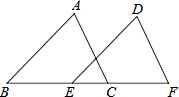如图，点B、E、C、F在一条直线上，∠B=∠DEF，AB=DE，BE=CF，∠F=70°，求∠ACB的度数．
画出数轴，在数轴上表示下列各数，并用“＜”连接：在-1，0，2，-3这四个数中，绝对值最小的数是（ ）
| A、-1 | B、0 | C、2 | D、-3 |
