题目内容
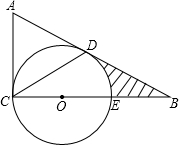 (2013•临沂)如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.
(2013•临沂)如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.(1)求证:∠A=2∠DCB;
(2)求图中阴影部分的面积(结果保留π和根号).
分析:(1)连接OD,求出∠ODB=90°,求出∠B=30°,∠DOB=60°,求出∠DCB度数,关键三角形内角和定理求出∠A,即可得出答案;
(2)根据勾股定理求出BD,分别求出△ODB和扇形DOE的度数,即可得出答案.
(2)根据勾股定理求出BD,分别求出△ODB和扇形DOE的度数,即可得出答案.
解答: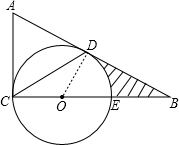 (1)证明:连接OD,
(1)证明:连接OD,
∵AB是⊙O切线,
∴∠ODB=90°,
∴BE=OE=OD=2,
∴∠B=30°,∠DOB=60°,
∵OD=OC,
∴∠DCB=∠ODC=
∠DOB=30°,
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∴∠A=2∠DCB;
(2)解:∵∠ODB=90°,OD=2,BO=2+2=4,由勾股定理得:BD=2
,
∴阴影部分的面积S=S△ODB-S扇形DOE=
×2
×2-
=2
-
π.
 (1)证明:连接OD,
(1)证明:连接OD,∵AB是⊙O切线,
∴∠ODB=90°,
∴BE=OE=OD=2,
∴∠B=30°,∠DOB=60°,
∵OD=OC,
∴∠DCB=∠ODC=
| 1 |
| 2 |
∵在△ABC中,∠ACB=90°,∠B=30°,
∴∠A=60°,
∴∠A=2∠DCB;
(2)解:∵∠ODB=90°,OD=2,BO=2+2=4,由勾股定理得:BD=2
| 3 |
∴阴影部分的面积S=S△ODB-S扇形DOE=
| 1 |
| 2 |
| 3 |
| 60π•22 |
| 360 |
| 3 |
| 2 |
| 3 |
点评:本题考查了含30度角的直角三角形性质,勾股定理,扇形的面积,勾股定理,切线的性质等知识点的应用,主要考查学生综合性运用性质进行推理和计算的能力.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
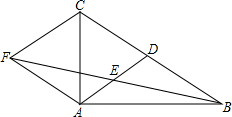 (2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(2013•临沂)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.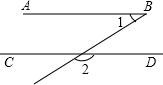 (2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
(2013•临沂)如图,已知AB∥CD,∠2=135°,则∠1的度数是( )
 (2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )
(2013•临沂)如图,四边形ABCD中,AC垂直平分BD,垂足为E,下列结论不一定成立的是( )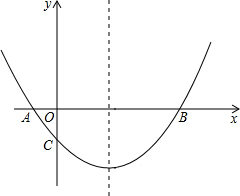 (2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,
(2013•临沂)如图,抛物线经过A(-1,0),B(5,0),C(0,