题目内容
【题目】如图,已知A是双曲线y= ![]() (x>0)上一点,过点A作AB∥x轴,交双曲线y=﹣
(x>0)上一点,过点A作AB∥x轴,交双曲线y=﹣ ![]() (x<0)于点B,若OA⊥OB,则
(x<0)于点B,若OA⊥OB,则 ![]() 的值为( )
的值为( ) 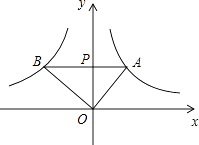
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:∵A点在双曲线y= ![]() (x>0)上一点,
(x>0)上一点,
∴设A( ![]() ,m),
,m),
∵AB∥x轴,B在双曲线y=﹣ ![]() (x<0)上,
(x<0)上,
∴设B(﹣ ![]() ,m),
,m),
∴OA2= ![]() +m2 , BO2=
+m2 , BO2= ![]() +m2 ,
+m2 ,
∵OA⊥OB,
∴OA2+BO2=AB2 ,
∴ ![]() +m2+
+m2+ ![]() +m2=(
+m2=( ![]() +
+ ![]() )2 ,
)2 ,
∴m2= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
故选C.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目