题目内容
若α,β都是锐角,下列说法正确的是
- A.若sinα=cosβ,则α=β=45°
- B.若sinα=cosβ,则α+β=90°
- C.若sinα>cosβ,则α>β
- D.若sinα<cosβ,则α<β
B
分析:一个锐角的正弦值等于余角的余弦值.正弦值随着角的增大而增大,余弦值随着角的增大而减小.故若sinα>cosβ,则α,β的关系不确定.
解答:根据一个角的正弦值等于余角的余弦值,判断A错误,B正确.
根据锐角三角函数的变化规律,则C,D错误.
故选B.
点评:注意正余弦的转换方法.也要注意特殊角的三角函数值和了解锐角三角函数的增减性.
分析:一个锐角的正弦值等于余角的余弦值.正弦值随着角的增大而增大,余弦值随着角的增大而减小.故若sinα>cosβ,则α,β的关系不确定.
解答:根据一个角的正弦值等于余角的余弦值,判断A错误,B正确.
根据锐角三角函数的变化规律,则C,D错误.
故选B.
点评:注意正余弦的转换方法.也要注意特殊角的三角函数值和了解锐角三角函数的增减性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
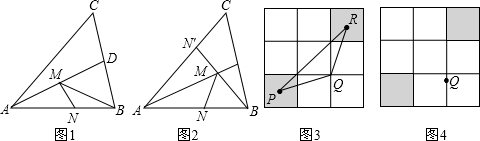
 ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是多少?