题目内容
图①是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.
(1)图②中阴影部分的正方形的边长是 _________ ;
(2)请用两种不同的方法求图2中阴影部分的面积:
方法1: _________ ;
方法2: _________ ;
(3)观察图②,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 _________ ;
(4)根据(3)中的等量关系解决如下问题:若m﹣n=﹣5,mn=3,则(m+n)2的值为多少?
(1)a﹣b (2)(a+b)2﹣4ab,(a﹣b)2 (3)(a+b)2﹣4ab=(a﹣b)2 (4)37
解析试题分析:(1)根据图形可知,阴影正方形的边长为小长方形的长与宽的差,写出即可;
(2)①从整体考虑,用大正方形的面积减去四个小矩形的面积就是阴影部分的面积;
②从局部考虑,根据正方形的面积公式,小正方形的边长的平方就是阴影部分的面积;
(3)把已知条件代入进行计算即可求解.
解:(1)阴影部分的正方形的边长是:a﹣b;
(2)方法1:大正方形的面积减去四个小矩形的面积:(a+b)2﹣4ab,
方法2:阴影小正方形的面积:(a﹣b)2;
(3)(a+b)2﹣4ab=(a﹣b)2;
(4)根据(3)的关系式,(m+n)2=(m﹣n)2+4mn,
∵m﹣n=﹣5,mn=3,
∴(m+n)2=(﹣5)2+4×3=25+12=37.
考点:完全平方公式的几何背景
点评:本题考查了完全平方公式的几何背景,以及两个公式之间的关系,从整体与局部两种情况分析并写出面积的表达式是解题的关键.

练习册系列答案
相关题目
 24、如图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
24、如图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均匀分成四块小长方形,然后按图2形状拼成一个正方形.
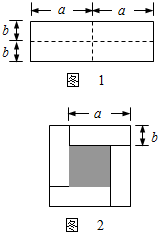 如图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
如图1是一个长为2a,宽为2b的长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形.
