Question

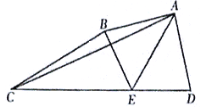
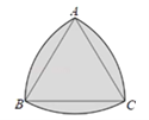
【题目】如图，分别以等边三角形 ABC 的三个顶点为圆心，以边长为半径画弧，得到的封闭图形就是“勒洛三角形”（勒洛 三角形是定宽曲线所能构成的面积最小的图形)，若 AB=2，则勒洛三角形的面积为( )

A. π+ B. π-C. 2π+2 D. 2π-2

Answer 1

【答案】D

【解析】

图中三角形的面积是由三块相同的扇形叠加而成，其面积=三块扇形的面积相加，再减去两个等边三角形的面积，分别求出即可．

解：过A作AD⊥BC于D，

∵△ABC是等边三角形，
∴AB=AC=BC=2，∠BAC=∠ABC=∠ACB=60°，
∵AD⊥BC，
∴BD=CD=1，

在Rt中，AD==，
∴△ABC的面积为：×BC×AD＝×2×=，
S扇形BAC==π，
∴莱洛三角形的面积S=3×π-2×=2π-2，
故选：D．