题目内容
已知抛物线y=ax2-(a+c)x+c(其中a≠c且a≠0).(1)求此抛物线与x轴的交点坐标;(用a,c的代数式表示)
(2)若经过此抛物线顶点A的直线y=-x+k与此抛物线的另一个交点为B(
| a+c |
| a |
(3)点P在(2)中x轴上方的抛物线上,直线y=-x+k与 y轴的交点为C,若tan∠POB=
| 1 |
| 4 |
(4)若(2)中的二次函数的自变量x在n≤x<n+1(n为正整数)的范围内取值时,记它的整数函数值的个数为N,则N关于n的函数关系式为
分析:(1)利用二次函数与x轴相交y=0,即可解决.
(2)首先表示出二次函数的顶点坐标,利用待定系数法求出.
(3)作PE⊥x轴于点E,PF⊥y轴于点F,利用三角函数关系解决.
(4)借助自变量的取值范围,代入二次函数解析式,即可解决.
(2)首先表示出二次函数的顶点坐标,利用待定系数法求出.
(3)作PE⊥x轴于点E,PF⊥y轴于点F,利用三角函数关系解决.
(4)借助自变量的取值范围,代入二次函数解析式,即可解决.
解答:解:(1)抛物线y=ax2-(a+c)x+c与x轴交点的横坐标是关于x的方程ax2-(a+c)x+c=0(其中a≠0,a≠c)的解.
解得x1=1,x2=
.
∴抛物线与x轴交点的坐标为(1,0),(
,0)
(2)抛物线y=ax2-(a+c)x+c的顶点A的坐标为(
,-
).
∵经过此抛物线顶点A的直线y=-x+k与此抛物线的另一个交点为B(
,-c),
∴
由③得c=0.
将其代入①、②得
解得a=-2.
∴所求抛物线的解析式为y=-2x2+2x.
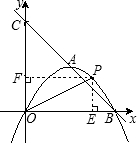
(3)作PE⊥x轴于点E,PF⊥y轴于点F.(如图)
 抛物线y=-2x2+2x的顶点A的坐标(
抛物线y=-2x2+2x的顶点A的坐标(
,
),
点B的坐标为(1,0),点C的坐标为(0,1).
设点P的坐标为(m,n).
∵点P在x轴上方的抛物线y=-2x2+2x上,
∴n=-2m2+2m,且0<m<1,0<n<
.
∴tan∠POB=
=
,tan∠POC=
=
.
∵tan∠POB=
tan∠POC,
∴m2=4n2.
解得m=2n,或m=-2n(舍去).
将m=2n代入n=-2m2+2m,得8n2-3n=0.
解得n1=
,n2=0(舍去).
∴m=2n=
.
∴点P的坐标为(
,
).
(4)N关于n的函数关系式为N=4n.
说明:二次函数y=-2x2+2x的自变量x在n≤x<n+1(n为正整数)的范围内取值,此时y随x的增大而减小,
∴-2n2-2n<y≤-2n2+2n,
其中的整数有-2n2-2n+1,-2n2-2n+2,-2n2+2n.N=(-2n2+2n)-(-2n2-2n)=4n.
解得x1=1,x2=
| c |
| a |
∴抛物线与x轴交点的坐标为(1,0),(
| c |
| a |
(2)抛物线y=ax2-(a+c)x+c的顶点A的坐标为(
| a+c |
| 2a |
| (a-c)2 |
| 4a |
∵经过此抛物线顶点A的直线y=-x+k与此抛物线的另一个交点为B(
| a+c |
| a |
∴
|
由③得c=0.
将其代入①、②得
|
解得a=-2.
∴所求抛物线的解析式为y=-2x2+2x.
(3)作PE⊥x轴于点E,PF⊥y轴于点F.(如图)
 抛物线y=-2x2+2x的顶点A的坐标(
抛物线y=-2x2+2x的顶点A的坐标(| 1 |
| 2 |
| 1 |
| 2 |
点B的坐标为(1,0),点C的坐标为(0,1).
设点P的坐标为(m,n).
∵点P在x轴上方的抛物线y=-2x2+2x上,
∴n=-2m2+2m,且0<m<1,0<n<
| 1 |
| 2 |
∴tan∠POB=
| PE |
| OE |
| n |
| m |
| PF |
| OF |
| m |
| n |
∵tan∠POB=
| 1 |
| 4 |
∴m2=4n2.
解得m=2n,或m=-2n(舍去).
将m=2n代入n=-2m2+2m,得8n2-3n=0.
解得n1=
| 3 |
| 8 |
∴m=2n=
| 3 |
| 4 |
∴点P的坐标为(
| 3 |
| 4 |
| 3 |
| 8 |
(4)N关于n的函数关系式为N=4n.
说明:二次函数y=-2x2+2x的自变量x在n≤x<n+1(n为正整数)的范围内取值,此时y随x的增大而减小,
∴-2n2-2n<y≤-2n2+2n,
其中的整数有-2n2-2n+1,-2n2-2n+2,-2n2+2n.N=(-2n2+2n)-(-2n2-2n)=4n.
点评:此题主要考查了二次函数与x轴的交点坐标,以及二次函数顶点坐标的表示方法,二次函数解析式的求法等,综合性比较强.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=