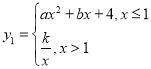题目内容
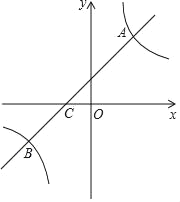
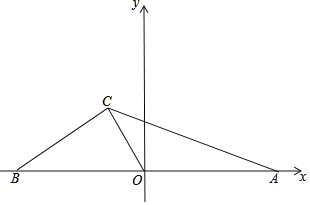
【题目】如图,在平面直角坐标系中,直线BC:y=![]() 交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,
交x轴于点B,点A在x轴正半轴上,OC为△ABC的中线,C的坐标为(m,![]() )
)
(1)求线段CO的长;
(2)点D在OC的延长线上,连接AD,点E为AD的中点,连接CE,设点D的横坐标为t,△CDE的面积为S,求S与t的函数解析式;
(3)在(2)的条件下,点F为射线BC上一点,连接DB、DF,且∠FDB=∠OBD,CE=![]() ,求此时S值及点F坐标.
,求此时S值及点F坐标.
【答案】(1)CO=5;(2)S=﹣2![]() t﹣5
t﹣5![]() ;(3)S=7
;(3)S=7![]() ,F坐标为(
,F坐标为(![]() ,
,![]() )或(
)或(![]() ,8
,8![]() ).
).
【解析】
(1)将点C坐标代入解析式可求m的值,由两点距离公式可求解;
(2)先求出点A坐标,用待定系数法可求CO解析式,可得点D坐标点D(t,﹣![]() t),由面积和差关系可求解;
t),由面积和差关系可求解;
(3)由中点坐标公式可得点E坐标(![]() ,﹣
,﹣![]() t),由两点距离公式可求t的值,即可求S的值,分两种情况讨论,由等腰三角形的性质和平行线的性质可求解.
t),由两点距离公式可求t的值,即可求S的值,分两种情况讨论,由等腰三角形的性质和平行线的性质可求解.
解:(1)∵直线BC:y=![]() x+
x+![]() 交x轴于点B,
交x轴于点B,
∴点B坐标(﹣8,0),
∵C的坐标为(m,![]() )
)
∴![]() =
=![]() ×m+
×m+![]() ,
,
∴m=﹣![]() ,
,
∴点C坐标为(﹣![]() ,
,![]() )
)
∴CO=![]() =5;
=5;
(2)如图,
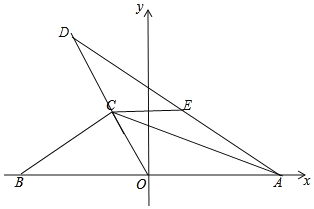
∵OC为△ABC的中线,
∴BO=AO=8,
∴S△ACO=![]() ×8×
×8×![]() =10
=10![]() ,
,
∵点C坐标为(﹣![]() ,
,![]() ),点O坐标(0,0)
),点O坐标(0,0)
设直线CO为:y=kx,
把C点代入得![]() =﹣
=﹣![]() ×k,
×k,
解得k=﹣![]()
∴直线CO解析式为:y=﹣![]() x,
x,
∴点D(t,﹣![]() t),
t),
∴S△AOD=![]() ×8×(﹣
×8×(﹣![]() t)=﹣4
t)=﹣4![]() t,
t,
∴S△ACD=S△AOD﹣S△AOC=﹣4![]() t﹣10
t﹣10![]() ,
,
∵点E为AD的中点,
∴S=![]() S△ACD=﹣2
S△ACD=﹣2![]() t﹣5
t﹣5![]() ;
;
(3)∵点D(t,﹣![]() t),点A(8,0),点E是AD中点,
t),点A(8,0),点E是AD中点,
∴点E坐标(![]() ,﹣
,﹣![]() t),
t),
∵CE=![]() ,
,
∴(﹣![]() ﹣
﹣![]() )2+(
)2+(![]() +
+![]() t)2=13,
t)2=13,
∴t1=﹣6,t2=﹣8,
∴点D(﹣6,![]() )或(﹣8,8
)或(﹣8,8![]() ),
),
当t1=﹣6时,则点F(﹣6,![]() ),S=﹣2
),S=﹣2![]() ×(﹣6)﹣5
×(﹣6)﹣5![]() =7
=7![]() ,
,
延长DF交x轴于点H,
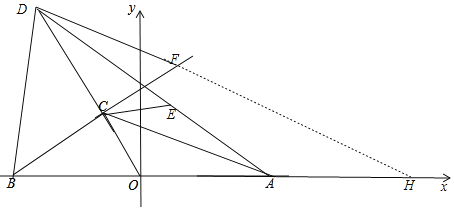
设点H(x,0)
∵∠FDB=∠OBD,
∴DH=BH,
∴x+8=![]()
∴x=20,
∴点H(20,0),
设直线DH的解析式为:y=kx+b,
∴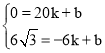
∴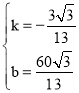
∴直线DH的解析式为:y=﹣![]() x+
x+![]() ,
,
联立直线DH和直线BC
∴![]() x+
x+![]() =﹣
=﹣![]() x+
x+![]() ,
,
∴x=![]() ,
,
∴点F(![]() ,
,![]() ),
),
当t2=﹣8,点D(﹣8,8![]() ),S=﹣2
),S=﹣2![]() ×(﹣8)﹣5
×(﹣8)﹣5![]() =11
=11![]() ,
,
∵点D(﹣8,8![]() ),点B(﹣8,0),
),点B(﹣8,0),
∴∠DBO=90°,
∵∠FDB=∠OBD=90°,
∴DF∥BO,
∴点F的纵坐标为8![]() ,
,
∴8![]() =
=![]() x+
x+![]() ,
,
∴x=![]() ,
,
∴点F(![]() ,8
,8![]() ).
).
综上所述:点F坐标为(![]() ,
,![]() )或(
)或(![]() ,8
,8![]() ).
).

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案