题目内容
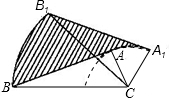（2013•盐城）如图，在△ABC中，∠BAC=90°，AB=5cm，AC=2cm，将△ABC绕顶点C按顺时针方向旋转45°至△A1B1C的位置，则线段AB扫过区域（图中的阴影部分）的面积为| 25π |
| 8 |
| 25π |
| 8 |
分析：根据阴影部分的面积是：S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1，分别求得：扇形BCB1的面积，S△CB1A1，S△ABC以及扇形CAA1的面积，即可求解．
解答：解：在Rt△ABC中，BC=
=
，
扇形BCB1的面积是=
=
，
S△CB1A1=
×5×2=5；
S扇形CAA1=
=
．
故S阴影部分=S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1=
+5-5-
=
．
故答案为：
．
| AC2+AB2 |
| 29 |
扇形BCB1的面积是=
45π×(
| ||
| 360 |
| 29π |
| 8 |
S△CB1A1=
| 1 |
| 2 |
S扇形CAA1=
| 45π×22 |
| 360 |
| π |
| 2 |
故S阴影部分=S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1=
| 29π |
| 8 |
| π |
| 2 |
| 25π |
| 8 |
故答案为：
| 25π |
| 8 |
点评：本题考查了扇形的面积的计算，正确理解阴影部分的面积=S扇形BCB1+S△CB1A1-S△ABC-S扇形CAA1是关键．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
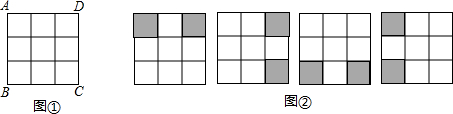
（2013•盐城）如图所示是一飞镖游戏板，大圆的直径把一组同心圆分成四等份，假设飞镖击中圆面上每一个点都是等可能的，则飞镖落在黑色区域的概率是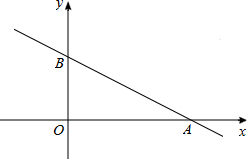
（2013•盐城）如图，在以点O为原点的平面直角坐标系中，一次函数y=-
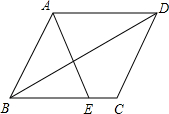（2013•盐城）如图，在平行四边形ABCD中，E为BC边上的一点，连结AE、BD且AE=AB．