Question

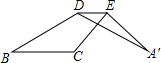（2010•集美区模拟）如图，将△ABC沿着它的中位线DE折叠，点A的对应点为A′，若∠C=120°，∠A=25°，则∠A′DB的度数是

110

度；若C点的坐标为（0，0），点B在x轴的负半轴上，A点的纵坐标为6，则A′点的坐标为

（2

3

，0）

．

Answer 1

分析：利用三角形的内角和为180°求出∠B，从而根据平行线的性质可得∠ADE=∠B，再由折叠的性质得出∠ADE=∠A'DE，利用平角的知识可求出∠A′DB的度数．以C为坐标原点，建立直角坐标系，过E作EF⊥x轴，再利用三角函数计算出CF的长，然后证明CE=A′E，再利用等腰三角形三线合一的性质算出A′点的坐标．

解答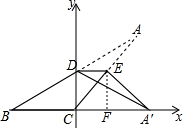：解：延长BD和CE相交于点A，
∵∠C=120°，∠A=25°，
∴∠B=180°-120°-25°=35°，
∵DE是△ABC的中位线，
∴DE∥CB，
∴∠ADE=∠B=35°，
根据折叠可得∠EDA′=∠ADE=35°，
∴∠BDA′=180°-35°-35°=110°．
以C为坐标原点，建立直角坐标系，过E作EF⊥x轴，
根据折叠可得A′点落在x轴上，
∵A点的纵坐标为6，
∴EF=3，
∵∠ACB=120°，
∴∠ACF=60°，
∴CF=

EF

tan60°

=

3

3

=

3

，
∵DE是△ABC的中位线，
∴CE=AE，
∵AE=A′E，
∴AE=CE，
∵EF⊥CA′，
∴CF=FA′=

3

，
∴A（2

3

，0）．
故答案为：（2

3

，0）．

点评：本题考查折叠的性质，注意掌握折叠前后对应角相等，对应线段相等，另外解答本题需要用到三角形的中位线，关键是掌握三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．