题目内容
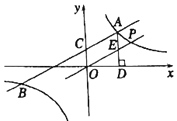
【题目】如图,一次函数y1=k1x+2与反比例函数y2=![]() 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.
(1)k1= ,k2= ;
(2)根据函数图象可知,当y1>y2时,x的取值范围是 ;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求直线OP的解析式.
【答案】(1)![]() ,16;(2)﹣8<x<0或x>4;(3)y=
,16;(2)﹣8<x<0或x>4;(3)y=![]() .
.
【解析】
(1)先把![]() 点坐标代入入
点坐标代入入![]() 可确定一次函数解析式,再把
可确定一次函数解析式,再把![]() 代入
代入![]() 可确定反比例函数解析式;
可确定反比例函数解析式;
(2)观察函数图象得到当![]() 或
或![]() ,一次函数图象都在反比例函数图象上方;
,一次函数图象都在反比例函数图象上方;
(3)先确定点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,再计算出
,再计算出![]() ,由
,由![]() 可求得
可求得![]() ,可求得
,可求得![]() ,则可求得
,则可求得![]() 的坐标为,然后确定直线
的坐标为,然后确定直线![]() 的解析式.
的解析式.
解:(1)把![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() ,
,
![]() 一次函数解析式为
一次函数解析式为![]() ;
;
把![]() 代入
代入![]() 得
得![]() ,
,
![]() 反比例函数解析式为
反比例函数解析式为![]() ,
,
故答案为:![]() ,16;
,16;
(2)![]() 当
当![]() 时即直线在反比例函数图象的上方时对应的
时即直线在反比例函数图象的上方时对应的![]() 的取值范围,
的取值范围,
![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() ;
;
(3)把![]() 代入
代入![]() 得
得![]() ,解得
,解得![]() ,
,
![]() 点
点![]() 的坐标是
的坐标是![]() ,而点
,而点![]() 的坐标是
的坐标是![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目