题目内容
(本题满分10分,其中第(1)4分、第(2)小题6分)
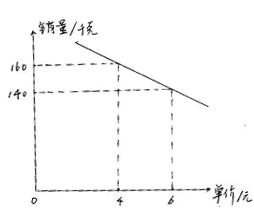
某公司销售一种商品,这种商品一天的销量y(件)与售价x(元/件)之间存在着如图所示的一次函数关系,且40≤x≤70.
(1)根据图像,求y与x之间的函数解析式;
(2)设该销售公司一天销售这种商品的收入为w元.
①试用含x的代数式表示w;
②如果该商品的成本价为每件30元,试问当售价定为每件多少元时,该销售公司一天销售该商品的盈利为1万元?(收入=销量×售价)
(1)y=-5x+600 (2)①-5x2+600x ②70
解析试题分析:解:(1)设函数解析式为y=kx+b(k≠0) (1分)
∵函数图像过点(50,350),(60,300)
∴ (1分)
(1分)
解得 (1分)
(1分)
∴y=-5x+600 (1分)
(2)①w=(-5x+600)·x
=-5x2+600x (3分)
②(-5x2+600x)-(-5x+600)·30=10000 (1分)
x2-150x+5600=0
(x-70)(x-80)=0
x1=70,x2=80(舍去) (1分)
答:当售价定为每件70元时,该销售公司一天销售该商品的盈利为1万元. (1分)
考点:一次函数的图像及性质,及销售问题。
点评:学会看清一次函数的图像及其性质,由图像中有两个坐标点可设一次函数的解析式代入即可求出,这是常用的待定系数法。根据销售量与售价可求出收入,需要注意的售价的取值范围,本题是图形与文字结合的题,要从中读懂有关信息,就可解出,属于中档题,难度一般。

(本题满分10分)宏远商贸公司有A、B两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
|
(1)已知一批商品有A、B两种型号,体积一共是20 m3 ,质量一共是10.5吨,求A、B两种型号商品各有几件?
(2)物流公司现有可供使用的货车每辆额定载重3.5吨,容积为6 m3,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
要将(1)中的商品一次或分批运输到目的地,宏远商贸公司应如何选择运送、付费方式运费最少?并求出该方式下的运费是多少元?
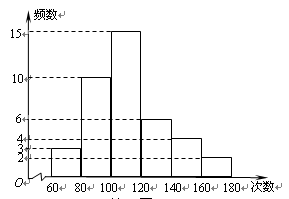
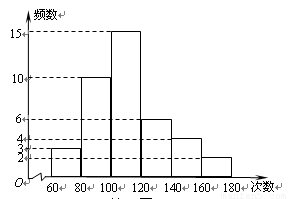
 秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点),那么
秒跳绳的成绩,列出的频数分布直方图如下(每个分组包括左端点,不包括右端点),那么